MicroStrategy增持比特币因逃避清算?首次抛售又为哪般?
来自 |TheBlock、blockworks
作者 |CaseyWagner、OsatoAvan-Nomayo
编译 |PANews
2022年12月28日,前MicroStrategy首席执行官Michael Saylor在社交媒体宣布该公司已增持约2500枚比特币。截至目前,MicroStrategy公司持有的比特币数量已经达到132,500枚,购买总金额超过40.3亿美元,平均购买价格约为30,397美元/BTC。
为什么MicroStrategy又双叒购买比特币?
Michael Saylor可以说是最直言不讳的比特币多头支持者之一,他此前曾表示购买比特币的决定是因为数字资产是金融的未来。由于MicroStrategy公司预计比特币价格会随着时间的推移而升值,因此相信从长远来看比特币将成为一种有效的通胀对冲工具。
Michael Saylor本人也多次将比特币称为“数字黄金”,更重要的是,通过投资比特币,MicroStrategy的知名度大幅提升,从一家“不起眼”的数据运营公司变成了加密爱好者们耳熟能详的名字,目前更是成为了全球持有比特币数量最多的美股上市公司。
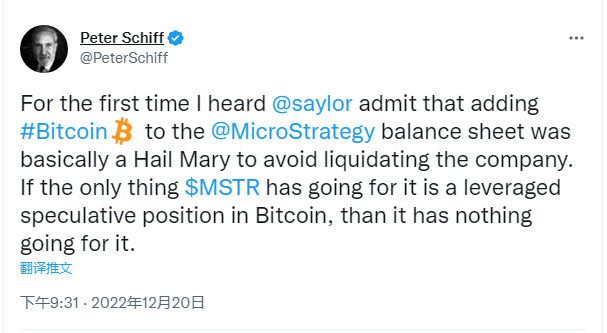
不过,他们购买比特币的“初心”可能并非真正出于认可加密和区块链技术。最近,经济学家PeterSchiff在社交媒体上披露了Michael Saylor和MicroStrategy投资比特币的真正原因,他指出Michael Saylor购买比特币是为了拯救MicroStrategy公司免于被清算,因为“除了对数字资产进行杠杆投机之外,该公司已别无他法。”
然而,MicroStrategy公司的问题还不限于此。
首次抛售比特币为哪般?
相较于购买2500 枚比特币,MicroStrategy公司首次抛售比特币尤其值得关注,因为Michael Saylor曾信誓旦旦承诺该公司永远不会出售其持有的比特币。
根据美国证券交易委员会本周三(12月28日)披露的文件显示,随着“税损收获(tax-lossharvesting)”交割最后期限的临近,MicroStrategy已经于2022年12月22日以1,180万美元的价格抛售了约704枚比特币,算上费用和支出,MicroStrategy最终每比特币获得收入约16,700美元。所谓“税损收获”,是指美国企业出售表现不佳的资产以实现损失并可能抵消收益的一种策略,但这些交易必须在每个日历年年底前完成。
美国证券交易委员会认为,MicroStrategy计划将此次交易产生的资本损失从之前的资本收益中扣除,因为根据目前执行的美国联邦所得税法,本次抛售比特币可能会给该公司带来税收优惠。显然,MicroStrategy首次抛售比特币的目的非常明显,他们想在纳税义务方面获益。
根据加密货币税收服务公司TokenTax会计师TynisaGaines透露,美国国税局禁止企业在30天内以亏损的方式出售证券,然后以“基本相同”的价格回购相同的资产,一旦企业执行此类交易操作,将会被美国国税局认定为“洗售交易”,这些公司不仅会受到处罚,而且永远无法就税收损失提出索赔。但是截至目前,该规则不适用于加密货币交易。
MicroStrategy似乎利用了这个“规则漏洞”,因为就在出售704枚比特币两天后的12月24日,该公司又以每枚16,845美元的价格购入约810枚比特币,总价值约1360万美元,而在11月1日至12月21日期间共计购入约2395枚比特币。
MicroStrategy在2020年转向比特币作为对冲通货膨胀的手段,但就目前来看,这种策略已经被证明是一场冒险的赌博,由于“加密寒冬”持续时间越来越长,比特币和许多加密货币不断下跌,MicroStrategy的市场表现也几乎坠入谷底。
即便Michael Saylor再次透露MicroStrategy将在 2023 年推出由比特币闪电网络提供支持的软件应用程序和解决方案以为加密生态系统做出更多贡献,希望重振市场信心,但自MicroStrategy周三公布增持比特币消息之后,该公司的股价并未出现复苏,反而下跌了约2%,整个2022年跌幅甚至超过了75%。
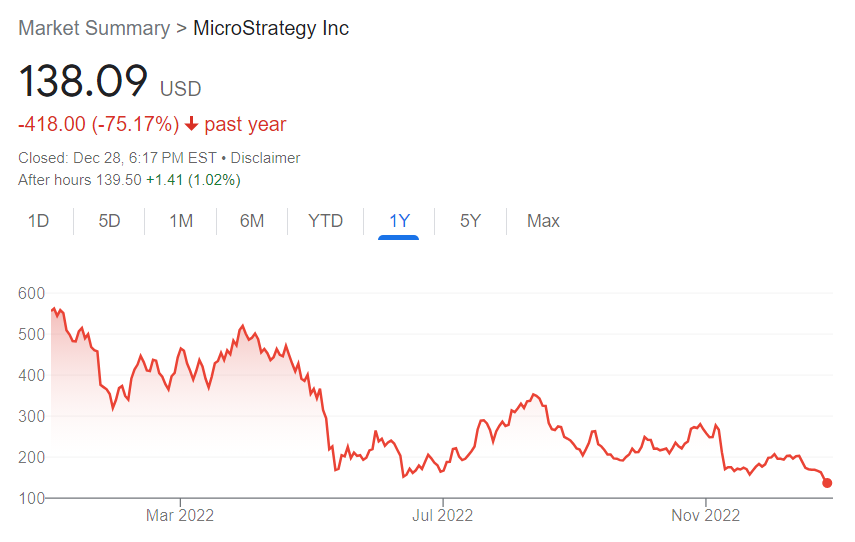
当然,现阶段而言,MicroStrategy还不太可能面临清算风险。根据Michael Saylor此前披露的信息,该公司有2.05亿美元的定期贷款,需要维持价值4.1亿美元的抵押品,但需要比特币跌至3,562美元才可能出现问题,短期内几乎不太可能看到这种情况。
持有比特币的MicroStrategy未来会尝试转型吗?
值得一提的是,MicroStrategy似乎开始从一家销售商业智能软件的公司尝试“低调”转型。今年八月,MicroStrategy在其官方网站发布信息招聘全职比特币闪电软件工程师,以构建一个基于闪电网络的SaaS平台,为企业提供应对网络安全挑战的创新解决方案,并支持新的电子商务用例。Michael Saylor也透露正在研究将大量用户接入比特币闪电网络的解决方案,包括但不限于闪电网络企业钱包、闪电网络企业服务器、企业身份验证服务等。
随着MicroStrategy寻求从常规软件应用扩展到比特币,其可以利用其现有的知识为企业提供比特币和闪电生态系统的工具,比如在线内容货币化、企业营销、网络付费墙和企业内部控制等。此外,MicroStrategy还计划举行以“企业闪电”议程为特色的比特币活动,该议程将更深入地探讨该公司的计划,即如何探索和贡献生态系统,并推动更广泛的采用。Michael Saylor在最新一期Twitter Spaces活动中透露,MicroStrategy公司已经开始启动相关方面的工作并希望在明年之前推出一些东西,预计第一季度会有所表现。
因此,在即将到来的2023年里,如果MicroStrategy真的官宣转型成为一家“比特币”公司,希望大家不要感到意外。