去中心化社交协议Nostr和Farcaster的区别是什么?
原文:《》by pourteaux
编译:DeFi 之道
长期以来,我一直在批评这样一种观点 : Twitter 是一个“城市广场”,在那里,适度管理被称为“审查”,用户有权成为平台会员,并成为受控制的受众。这一立场的支持者几乎将 Twitter 视为一种实用工具,并认为限制该平台的活动实际上是对言论的违宪限制。令人惊讶的是,这是现代“新浪潮”自由意志主义的观点,其支持者声称 Twitter 由于其不可逾越的网络效应而具有垄断地位,因此不值得为私营公司提供典型的保护。

私营公司从来都不是城市广场, 但协议可能是。
我赞成老牌自由主义者的观点:Twitter 是一家私营公司,它制定了自己的服务条款,政府不应该代表 Twitter 做出运营决策。任何人都不应有权获得私营公司的服务,并且在不向特定平台的受众提出要求的情况下,存在无限的言论自由场所。显然,将仇恨言论平台化对 Twitter 的业务不利,因为他们会失去广告商。认为你无法与 Twitter 竞争的想法是荒谬的,它有很多社交网络竞争对手,例如 Facebook 和 TikTok,它还有直接竞争对手,例如 Gab、Mastodon、Truth Social 等。
新浪潮自由主义者争辩说,那些被禁止使用 Twitter 的人“不能就这样开始他们自己的社交网络”,但这实际上是前总统在 1 月 6 日被禁止后对 Truth Social 所做的。此外,很多声称“审查”的人实际上拥有巨大的平台,通常会把“审查”的说法作为一种民粹主义的增长手段。
作为一家私营公司,Twitter 不仅有权以他们认为合适的方式对言论进行审核,而且精心策划的平台可以使 Twitter 成为拥有更好的用户体验以及更有利可图的业务。几乎没有人希望自己的 Twitter 时间轴上有 4chan 的东西。马斯克在接管 Twitter 时帮了我们所有人一个忙,他迅速向右翼证明了这一点:这个承诺“放飞 Twitter ”的男人,他限制言论的程度,与 Twitter 的前任领导层一样多,甚至要更多。他更冲动地做这件事,用的程序更少,并且是出于中间偏右的偏见,但关键是他这样去做了。没有审核的 Twitter 一直是站不住脚的, 一家私营公司无法创建一个真正畅通无阻的言论平台,当他们尝试时,平台就变成了几乎所有人都忽视的污水池,而且没有商业模式,就像 4chan 一样。
既然如此,你可能会想知道——为什么我会提倡一个开放的、无需许可的和抗审查的社交网络?
新的社交层使我们能够满足那些想要完全开放的“城市广场”的人,以及那些优先考虑精心管理和策划体验的人。 这两种观点看似对立,实际上却完全一致。 事实上,我不认为这两种说法所代表的群体有任何分歧,他们只是注意到了现代社交网络功能障碍的不同部分。在过去几年里,私营公司一直在努力成为言论自由的捍卫者,也试图成为拥有基本礼仪规则的地方,但都以失败告终。
你不能两者兼得。 政府、广告商、员工和公众压力将迫使私营公司限制言论。 而且,任何管理行动在未来都可能被滥用,并可能剥夺很多人的权利。
私营公司不能成为公共广场,但协议却可以。
像 Nostr 或 Farcaster 这样的协议可以是无需许可和抗审查的,因为在一个分布式网络中,没有人可以向其发送删除请求。当然,这是一个尚未完善的的解决方案,因为如果你停在这里,那么你得到的只有一个分布式的 4chan ,这基本没有人会感兴趣。你需要一个第二层的私盈公司和客户来充当策展人和版主。用户可以选择加入并为这个管理层付费,以提供更好的体验。根据你的世界观,你可以从《纽约时报》或 《Joe Rogan Experience》 的第 2 层策展付费。Twitter 本身可能是来自 Nostr 或 Farcaster(或两者)的内容策展人,并在内容旁边为你提供广告以使平台免费。所有这些不同的 L2 运营商的审核决策可能会有一些重迭,但也会有很多不重迭的审核决策。因此,没有人有被“去平台化”的风险,除非你完成了同时被所有不同的 L2 管理者禁止的不可能的任务。即便如此,对于那些能够忍受的人来说,这样一个人的帖子仍然可以在未经审核的 L1 上看到。
因此,“社交层”解决了政治光谱双方的需求:一个无需担心“审查制度”和“去平台化”的社交平台,同时还允许用户选择加入他们信任的版主的精选体验!
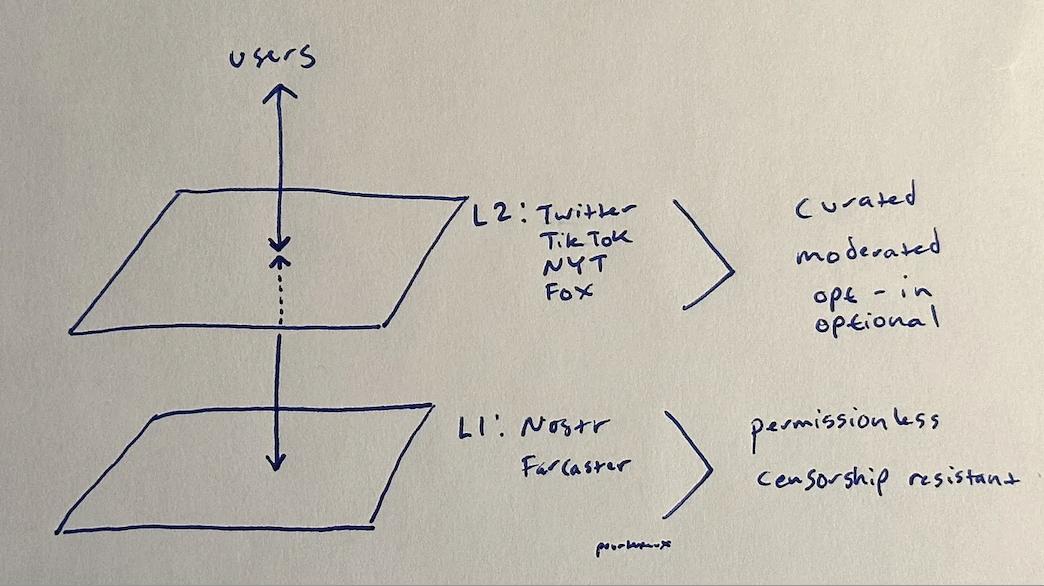
社交层允许无需许可和抗审查的 L1 的所有好处,以及 L2 中可选的策划体验的所有好处。
让我们深入探讨 L1 的两种尝试:Nostr 和 Farcaster。 我很高兴同时使用这两者,并将提供我对两者的非技术经验以及我所看到的潜力和局限性。 我还要感谢 fiatjaf(建立了 Nostr)帮助我理解了 nostr,感谢 Dan Romero(Farcaster 的创始人)邀请我加入 Farcaster。 我还要感谢 Maciek Laskus,他对每一个问题都进行了透彻的分析,并就该主题与我进行了交谈。 让我们从一张表开始:
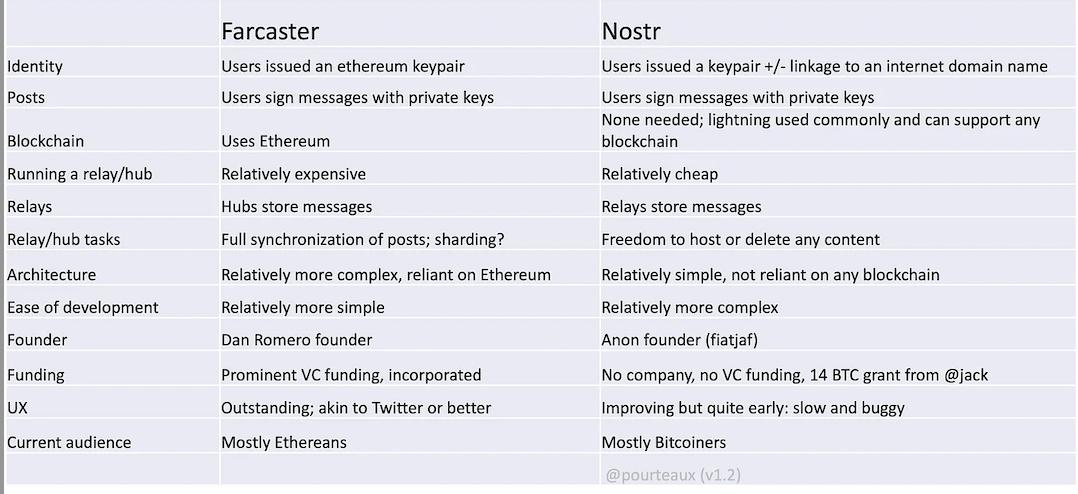
Farcaster 和 Nostr 都旨在去中心化通信,但在此过程中做出了不同的权衡。
Nostr 和 Farcaster 都使用中继器(在 Farcaster 中称为“ hubs”)来存储社交数据(如帖子)并将其传输给用户(用户运行的软件称为“客户端”)。 Farcaster 使用以太坊架构(例如,账户使用以太坊密钥对),而 Nostr 不使用区块链(尽管你看到很多闪电网络交易,但理论上它可以支持任何区块链)。
值得注意的是,Farcaster 是一家由 VC 支持的公司,其拥有知名的团队以及出色的产品,而 Nostr 根本不是一家公司,它是由一个没有资金的匿名者建立的(尽管后来从 Jack Dorsey 那里获得了 14 BTC 的资助),而且明显处于更早的开发阶段。 在与 fiatjaf 交谈时,我确认 Nostr 的唯一资金是 Jack 提供的这笔比特币赠款,fiatjaf 随后与 jb55 分道扬镳,后者正在 iOS 和 macOS 上开发 Damus 客户端。 Farcaster 和 Nostr 都已经在上面构建了客户端和服务(示例:Nostr、Farcaster),尽管 Farcaster 似乎在这个过程中走得更远。 事实上,Farcaster 做出的一些设计选择使开发更容易,而 Nostr 的简单性,是在近期困难的开发与更多的未来潜在用例之间进行了权衡。
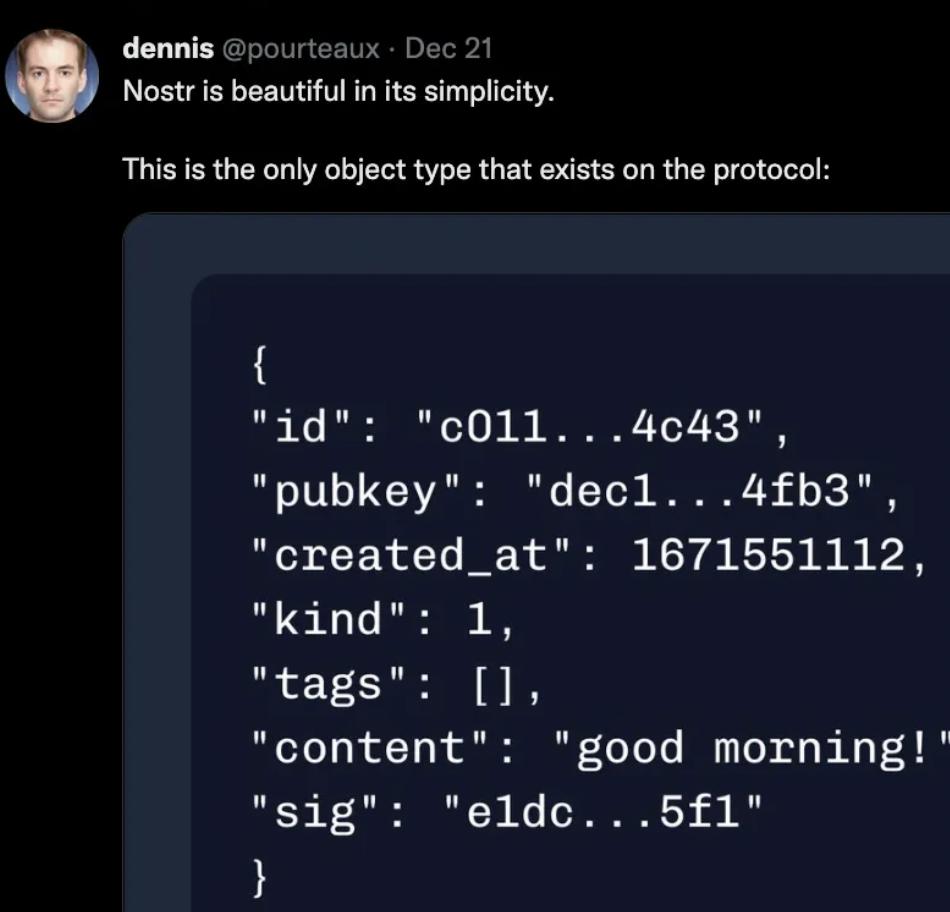
例如,Farcaster 目前需要网络中所有 hubs 的完全同步,这使得开发客户端更加容易。 相比之下,Nostr 允许中继器托管或删除任何内容,这使得客户端开发在短期内更加困难,但允许为这些中继器提供许多潜在的商业模型以及更多开放式的潜在用例。 Nostr 上的中继器随后可以收取订阅费或投放广告或以其他方式选择要包含和排除的内容。
Farcaster 已经为普通用户准备了一款精美的产品, 该应用程序与 Twitter 一样好用,甚至会更好。
Nostr 目前的用户群主要是比特币用户,而 Farcaster 的用户群主要是以太坊用户以及科技企业家。 在很多方面,这也体现在每个平台的设计选择上。 与比特币一样,Nostr 优先考虑简单性、中立性以及运行你自己的中继器(如比特币中的节点)的便利性。 与比特币一样,Nostr 避开风险投资,成立公司或拥有知名创始人。 使用 Farcaster 运行一个 hub 要更加困难和昂贵,但 Farcaster 断言称,某些设计权衡仍然允许“充分的去中心化”,同时优先考虑更近期的用例以及几乎为零售用户准备好的优化产品。
我在两个平台上都有一个账号(Nostr上的@pourteaux.com, Farcaster上的@px)。简单地说,Nostr 似乎遵循了密码朋克和比特币的精神,其中简单性和稳健的协议是最重要的。fiatjaf、jb55 和其他贡献者给我留下了深刻的印象。Farcaster 遵循的是一种更为传统的科技初创公司模式,他们的产品经过精心打磨,现在看起来很令人愉悦。这两项努力都是为了为互联网创造一个原生的社交层 : 我认为这是一项道义上的义务。如此多的社会功能失调,是我们当前企业社会层试图为所有人提供所有东西的结果。社交媒体的分层方法,将 L1 中的密码朋克原则与 L2 中机构的重要性结合起来,以服务于满足每个人需求的社交体验。