5天倒计时,读懂隐藏在周期里的比特币「减半」密码
伴随着减半临近,今年「现货比特币 ETF、比特币减半、美联储降息」的三大利好即将兑现过半。
撰文:River
2024 年,市场对今年最为期盼的三大明确利好中——现货比特币 ETF、比特币减半、美联储降息,第一个已然落地,并推动比特币突破 7 万美元,创下历史新高。
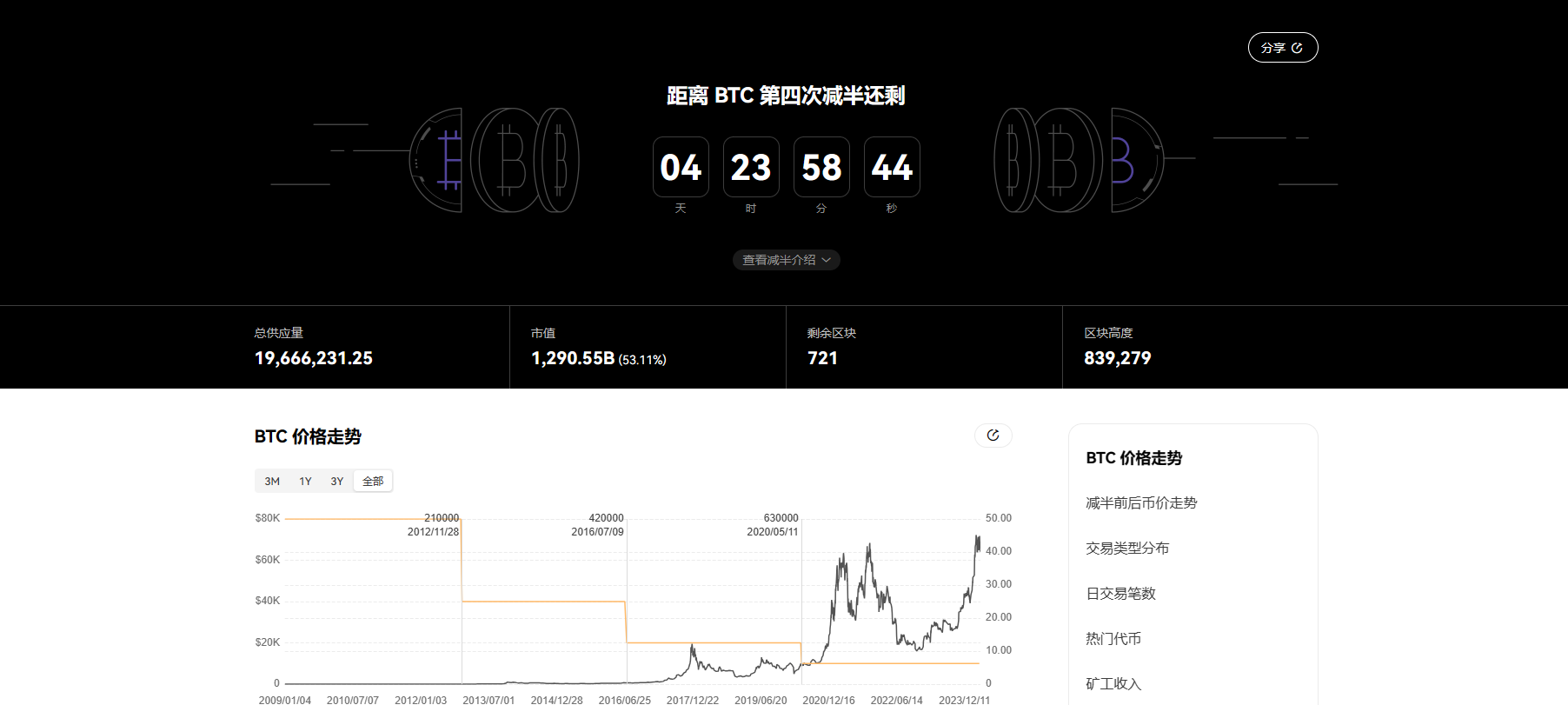
如今伴随着减半的临近,今年的三大利好即将兑现过半,可能会对新一轮市场演变造成影响——OKLink 统计数据显示,目前据第四次比特币减半的时间已剩余不足 5 天,预计为 2024 年 4 月 20 日,届时区块奖励将从 6.25 BTC 降至 3.125 BTC。
作为加密行业最重要的叙事之一,「比特币减半」一直是市场抱有巨大期盼的重要刺激事件,面临着新一轮减半周期走向尾声,2024 年的我们又该抱有怎样的期待,市场上又出现了哪些新的变量?
减半对加密市场有何影响?
我们可以简单了解下比特币减半的基础知识:比特币的机制设计决定了矿工的角色异常重要,是维系整个系统交易运作的基石,而目前矿工的收入主要来源于两部分——区块奖励和手续费。
其中区块奖励开始是 50 个比特币,规则是每四年减半一次,目前已经减半过三次是 6.25 个,5 天后就是第四次减半,而到 2140 年比特币就不再有区块奖励;
但手续费则会一直存在,所以说将来矿工的收入就将变得很单一,只有手续费奖励,也正因如此,加密行业一直是周期性最强的行业之一。
从历史角度看,每轮减半都是一次盛事,尤其是比特币第一次减半周期,出现了数十倍的惊人涨幅。以 OKLink 统计的「减半前后币价走势」为例:
- 第一次减半(2012 年 11 月 28 日)发生 132 天后,BTC 累计涨幅高达 2361%,创下历史新高。
- 第二次减半(2016 年 7 月 9 日)发生 1 年 5 个月后(期间诞生了繁荣的 ICO 浪潮与打断进程的「9·4」事件,因此周期较长),BTC 累计涨幅高达 2804%,创下历史新高;
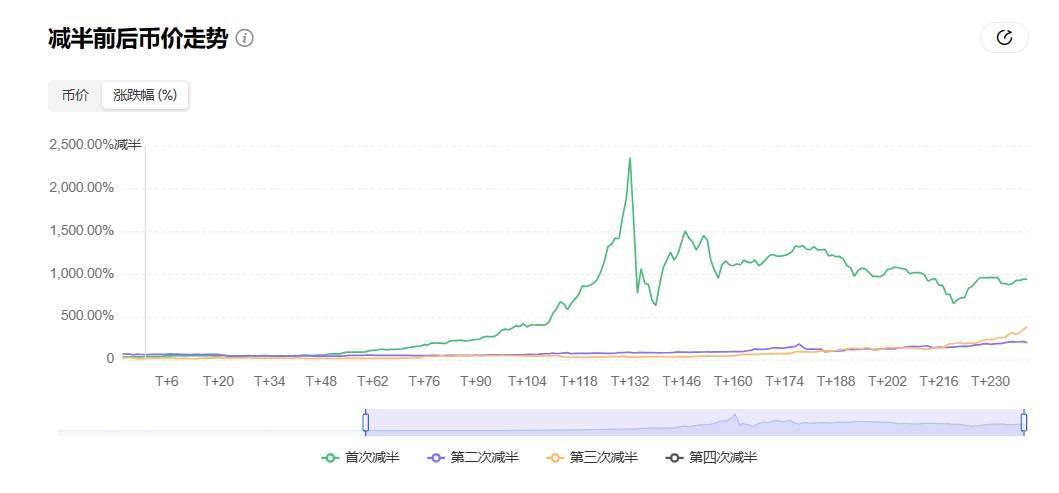
不过 2020 年第三次减半开始,由于行业从业人数、市场关注度以及配套基础设施的完善性都比之前有了显著的提升,比特币再也不是局限在极客圈子的小众产品,体量规模再难达到数十倍的涨幅,因此相较于减半节点只上涨了约 7 倍。
简单地概括:
第一次减半之前,圈内极客们更关心的是比特币作为电子现金的可能性;
第二次减半周期中,关于比特币的关注点转变到了其成为支付工具的属性,也引发了一系列争论(随后的 BCH 分叉几乎是圈内的顶流);
而在第三次减半周期,比特币已经成为一种另类资产,关注传统机构与资本的布局开始成为主旋律;
所以虽然价格变化幅度不如此前两次减半,但比特币第三次减半的热度则是空前的,与此同时,比特币第三次减半时世界整体政经环境也影响了它的表现:
在宏观因素的影响下,5 月 11 日减半前两个月的 3 月 12 日 ——3 月 13 日,比特币从 7600 美元开始一路下行,先是跌至 5500 美元震荡。后续更一路下破支撑点位,最低下探到 3600 美元,整体市值转瞬蒸发 550 亿美元,全网爆仓 200 多亿人民币,精准实现了「价格减半」。
不过随后在 5 月减半后,DeFi 盛夏开启了新一轮的牛市周期,比特币也直冲 6 万美元,相比减半时翻了将近 7 倍。
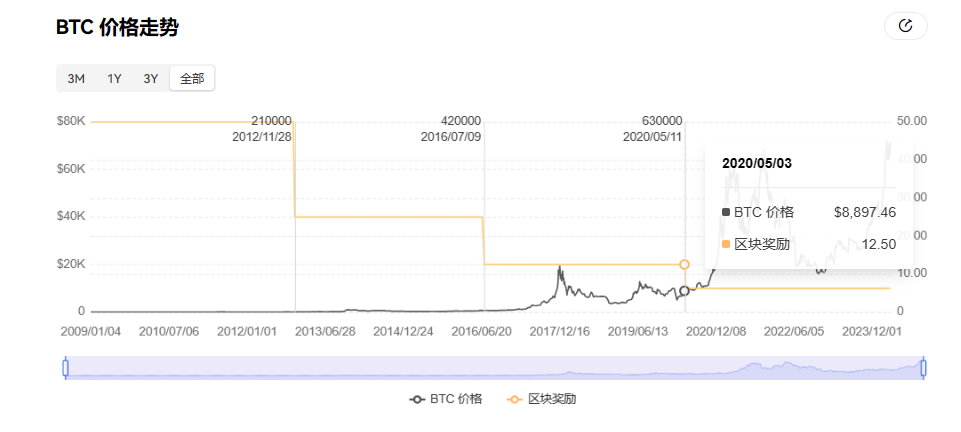
总的来看,从历史经验来看,减半后的半年到 1 年时间内,BTC 极有可能开启一轮新的牛市周期,如今的体量或许较难在实现 10 倍以上的涨幅,但超越 10 万美元甚至 20 万美元的整数级关口还是相当值得期待。
减半之外的新变量
不过与此同时,在比特币已经历经三次减半,区块奖励降为 6.25 个、已挖出数量达 1900 万以上的大背景下,其实很多情况、很多事情也到了换一个新视角重新思量的时候了。
尤其是整个行业以及比特币自身相比之前几次减半都出现了一些值得关注的新变量。
矿企军备竞赛的加剧
众所周知,圈内资本向来喜欢集体豪赌「减半盛事」,不断增长的算力、新硬件、即将到来的奖励减半等因素将决定行业和比特币的总体增长,如今更是如此:
而截至最新一次比特币于区块高度 836640 进行的挖矿难度调整——挖矿难度达 83.13T,相比一年前几乎翻了近一倍。
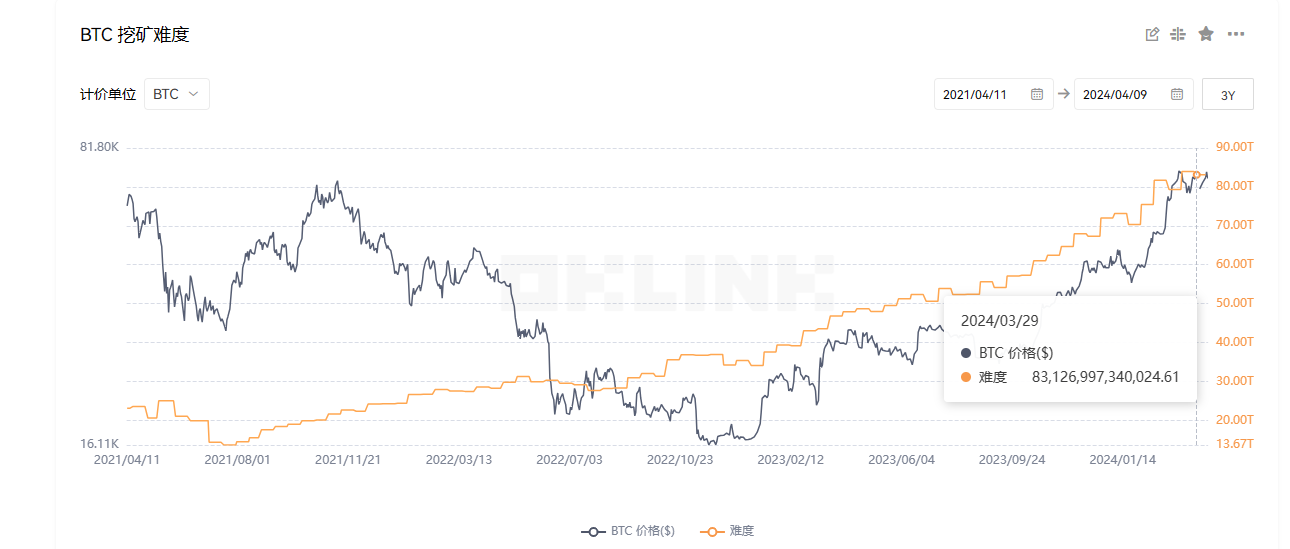
在此背景下,过去一年飞涨一倍的全网算力,叠加 10 天后减半导致矿工能挖出的比特币数量锐减 50%,意味着矿工们为了维持自身的运营现金流保持稳定,必须被迫加大算力投入,以挖出足够的 BTC 来覆盖开支。
这会进一步导致网络算力显著增加,挖矿难度不得不将向上调整以保持 BTC 生产速率稳定,从而将成本较高的矿工挤出市场。
根据 CoinShares 研究报告显示,10 天后减半完成之际,矿工的比特币生产平均成本或将大幅上升,成本中位数为 42000 美元以上,不过由于近 2 个月来比特币价格的飙升,目前绝大部分矿工的生产成本都低于市场价格。
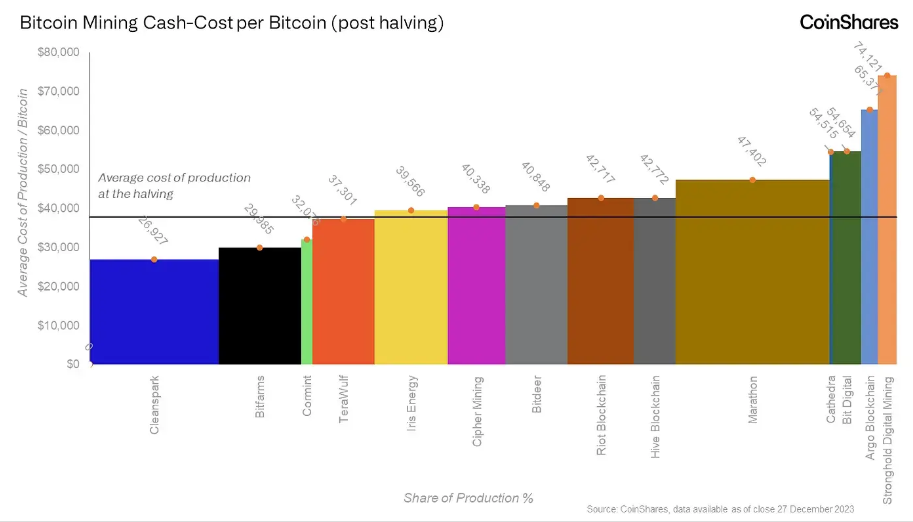
因此不排除此次减半会出现例外,即全网算力会以更陡的斜率飞速增长——自 2012 年第一次比特币减半,以及随后的 2016 年和 2020 年减半以来,减半后算力通常会下降约 9%,这种情况通常会持续六个月左右,随后中途复苏,然后在下一次减半前大约一年出现活动激增。
这个周期是合乎逻辑的:为了在减半的预期中保持竞争力,矿工增加了资本支出,使算力显著高于趋势。减半后,矿工的直接收入减少,影响了他们的资本支出周期。
矿工们本质上是在进行军备竞赛,以购买和增加尽可能多的机器,而此次的「市场价格>挖矿成本」变量,究竟会对矿工市场及比特币二级市场产生怎样的联动影响,尚需持续观察。
比特币生态的内部演化
根据比特币的减半规则,区块奖励开始是 50 个比特币,规则是每四年减半一次,目前已经减半过三次是 6.25 个,这样一直持续减下去,到 2140 年比特币就不再有区块奖励;
而手续费则会一直存在,所以说伴随着一轮轮减半之后,区块奖励会逐步减少乃至趋近于无,将来矿工的收入就将变得很单一,只有手续费奖励。
而 2023 年以来比特币生态尤其是 BRC20 的繁荣,掀起了「BitcoinFi」的新浪潮,比特币生态内部交易的活跃达到新峰值,从而助推比特币的手续费收入激增——目前仅 ORDI、SATS、RATS 这三个新资产的总市值就将近 30 亿美元,总持仓地址数超 9 万个。
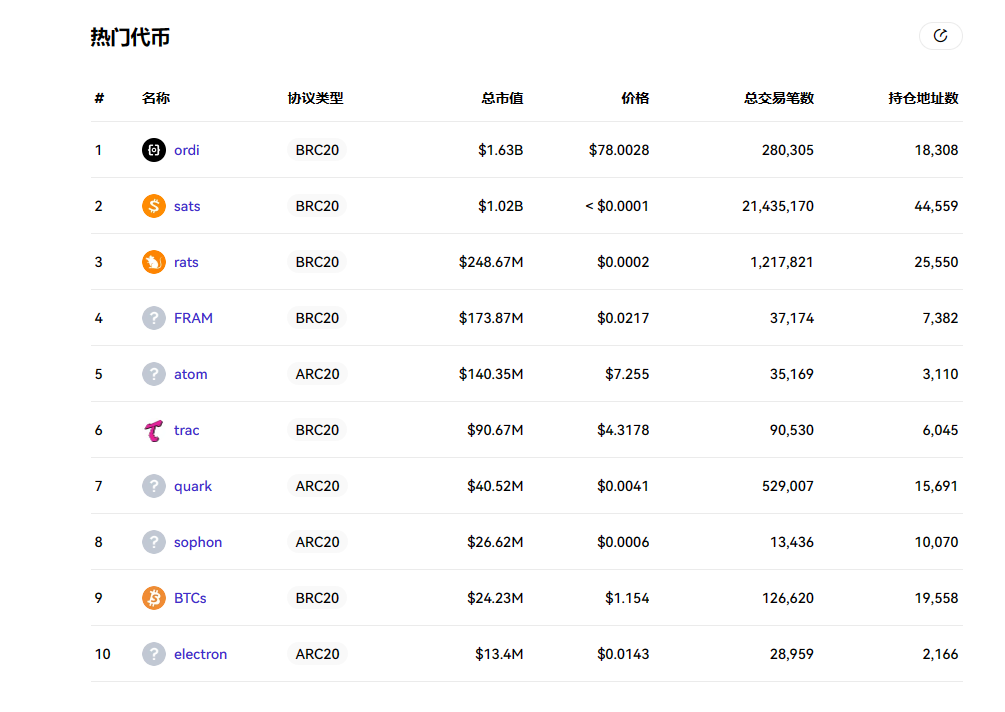
这波 Ordinals 浪潮将天量的资金、用户、开发者通过铭文这条管道引入比特币生态:如果说以前的比特币只有占有「道统认知」和总市值优势,铭文潮则直接大幅度提高了比特币生态的新资产丰富度,人类对新资产的需求是永恒存在的,同时它也间接提高了开发者数量和用户基数。
在此背景下,Ordinals 等协议创新伴随着 ORDI、SATS 等龙头项目的攻城略地,深度影响了比特币网络的费率模型——最直接地,就是彻底改变了比特币的经济模型和激励模型。
OKLink最新数据显示,目前 Ordinals 交易占比特币链上总交易的比例,从 2023 年年初的 0 开始起步,如今已经基本稳定在 50% 以上。
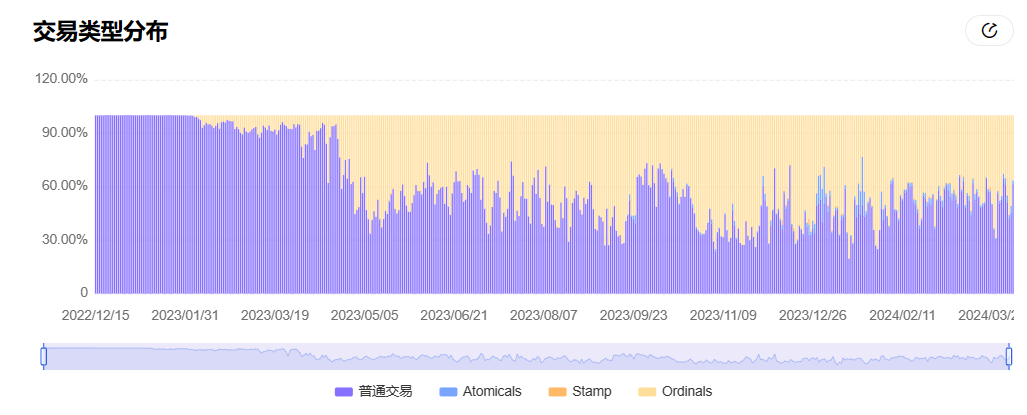
这也助推 BTC 挖矿手续费收益创近 5 年来新高,要知道此前矿工手续费收入的历史平均数据往往占比只有 2% 左右,去年底甚至一度高达 40%(近三个月有所回落)。
随着后续区块奖励逐步递减直至趋于零,那么手续费重要性就会越来越高,直到最终成为唯一收入来源。
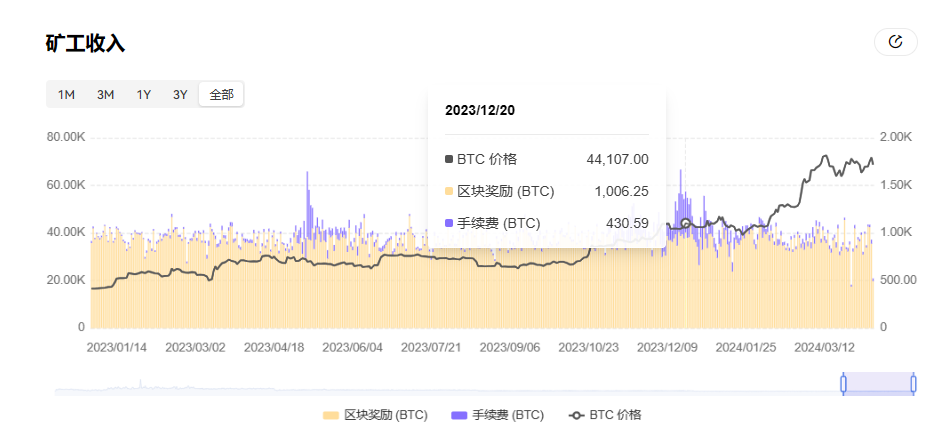
所以这一轮 BRC20 相当于提前做了一次预演,后续无论是否成功,伴随着后续比特币减半的发生,这条路上的变量势必会深刻改变比特币的整体费率模型。
小结
总的来看,现在我们则处在新一轮减半周期的尾声,这也可能是绝大部分此轮从业者和投资者入圈第一次(或第二次)亲身见证并经历的比特币减半「盛事」。
凡是过去,皆为序章。作为加密行业最重要的叙事之一,「比特币减半」一直是提振市场信心的良药,如今牛的脚步若即若离,接下来减半后比特币及本轮周期会如何走向,还是未知之数。