USV观点：NFT虽经泡沫但终成社交原语，经久不衰

作者：

编译：Felix, PANews

自互联网诞生以来，数字商品的内涵一向广泛，所有权的概念只存在于中心化的封闭系统范围内。公共区块链的出现，解锁了拥有独特且完全由个人拥有数字物品的能力——这个概念在今天与六年前一样强大。数字时代下，所有权和可验证的来源是革命性的，而如今只触及到数字浪潮所带来影响的表面。

泡沫

NFT于2017年爆发，正如许多人可能已经注意到的，在接下来的几年里发生了很多事情。以下是二级市场所有公链上每周NFT交易量的视图：

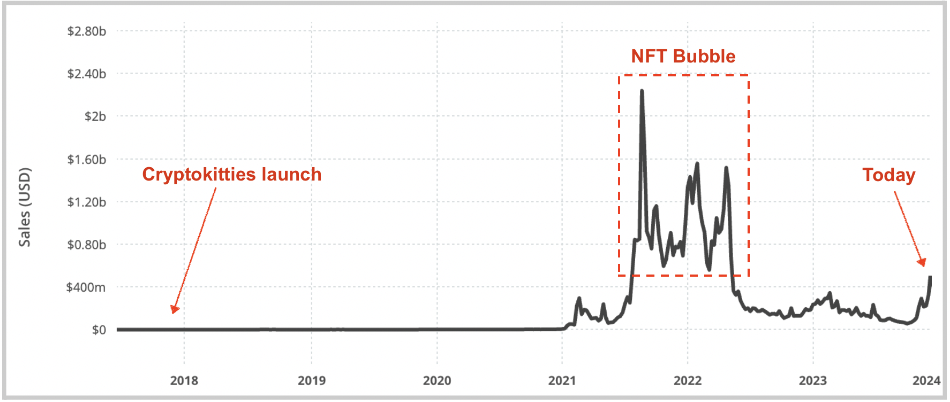
USV观点：NFT虽经泡沫但终成社交原语，经久不衰

所有公链的月度二级市场交易量在2022年1月达到约60亿美元的峰值，在2023年10月达到约3亿美元的最低点，上个月反弹至约17亿美元，其中比特币和Solana生态显著增长。

NFT，特别是作为收藏品的NFT，经历了以资产泡沫为标志的大规模炒作周期。泡沫破裂后价格和二级市场交易量急剧下降，分别下降了85%和95%以上。由于市场在2021年处于极度风险的零利率环境中，NFT出现剧烈的涨跌。

这个故事听起来很熟悉，因为几乎每一项新兴技术的发展均是如此。NFT是更大的加密生态的一个缩影，二者最近都经历了非理性繁荣时期。在Carlota Perez的框架下(注：经济理论学家，研究过自工业革命以后所有主要技术革命，深知它们是如何被影响，以及它们如何影响资本市场)，我们似乎正在经历这些技术的建设阶段，其中核心基础设施正在构建。

尽管经历了这段“狂热”和价格崩溃时期，但NFT的前景仍未改变。NFT是一种创新的载体，一种代表数字生活中不可替代部分的新工具——门票、会员资格、收藏品、收据、艺术、媒体、点赞。

在作者看来，如今在加密领域看到的各种泡沫，包括NFT狂热，是重大技术变革显现和成熟的正常和不可避免的一部分。该时期还提供了一个直接的好处：投机市场泡沫在一定程度上提供了建设下一阶段基础设施所需的资金。

创新

加密市场的起起落落有助于揭示该领域的问题，例如交易成本过高和普通用户的可用性差，而剧烈的价格波动也有助于为这些问题的解决方案提供资金，并推动了建设和创新步伐。

在经过区块链技术多年的发展，许多Layer2区块链进入市场，以更快的速度开辟了更便宜的区块空间，同时保留了以太坊的安全保证。Solana推出了压缩NFT，允许开发人员和用户以约百分之一美分的成本创建NFT。嵌入式钱包提供了一种在不牺牲去可信性的情况下构建低摩擦加密dApp的方法。像ERC-6551这样的新标准允许NFT本身充当帐户/钱包，为NFT开辟了设计空间。像Arweave这样的网络已经成熟，并且在很大程度上解决了在链上存储任意内容（不仅仅是元数据）的问题。

这些改进的最终结果是，NFT所适用范围正在迅速扩大，与NFT的交互变得越来越便宜和容易。在许多情况下，现在有工具可以将技术抽象出来，让用户参与到由NFT支持的数字体验中。艺术品和收藏品只是拼图的一小部分，如今生活中的任何数字制品都可以——而且最终可能会——由NFT来代表。

艺术品和收藏品

包括艺术品在内的数字收藏品是NFT最初在区块链上表达自己的方式，也是最初被采用的方式。他们仍然是NFT的一部分，迄今为止，NFT的几乎所有交易额和市值都由他们占据。尽管存在资产泡沫，但NFT不会消失。

对于数字艺术家和创作者来说，NFT是一个巨大的解锁器，他们现在可以将自己的作品代币化，并满足对数字创作日益增长的需求。收藏家、投机者和赞助人最终都可以拥有独特而稀缺的数字物品，并且无需许可地转让。这反过来又为这些资产创造了充满活力的市场。区块链提供的网络原生金融通道也使创作者更容易向全球出售作品。区块链还催生了新的艺术形式，并与创造性工作（如随机性）互动的同时产生新的元素。

此外，生活在数字世界里，网络原生资本稳步增长（多亏加密货币），数字创作越来越无处不在（多亏AI）。这些趋势的逻辑终点是让更多人在更广泛的数字对象中存储更多价值。

行为转变

尽管交易活动和市值严重下降，但加密创造速度仍然强劲。每个月都有成千上万的创作者在创作数字艺术、生成艺术或AI艺术。每个月，新的（和现有的）加密用户都会从这些收藏品中铸造作品。

此外还看到新的NFT行为出现。通常零成本的公开铸造在整个2023年越来越受欢迎。示例用法是，项目推出产品时在一定时间内发布公开版集合，用户选择铸造NFT并不是一种投机行为，而是一种表达支持的方式（一种可能从中受益的赞助行为）。在某些情况下，低成本或无成本的铸造正逐渐成为类似于“点赞”或“转发”的一种新的社交原语。

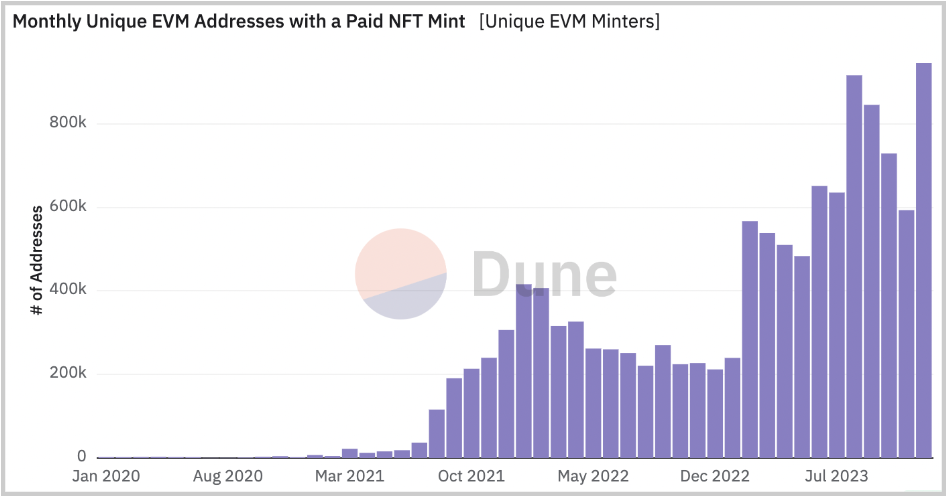
这些新行为促使低成本铸造的持续增长。数据显示，尽管2023年二级交易量降低，但有更多用户铸造比以往更多的NFT。

通过压缩（即 Bubblegum）解锁Solana铸造的

NFT就是一切

这篇文章的大部分内容都集中在NFT的特定部分及其复兴和发展上，但现实是NFT是一个可以代表几乎任何事物的典范。

以太坊系统使用NFT来表示身份。Uniswap使用NFT来表示给池提供流动性。Web3餐厅平台Blackbird将用户与餐厅的每个关系表示为NFT。Helium协议中NFT代表了可以获得网络奖励的资格（NFT可作为网络凭证并验证热点）。此类例子不胜枚举。

而作者也乐于见到更多行为和物品被表示为NFT。从音乐会到电影再到航空公司的所有门票都应该是NFT，包括任何可以从真正所有权和开放、永久系统中受益的东西。

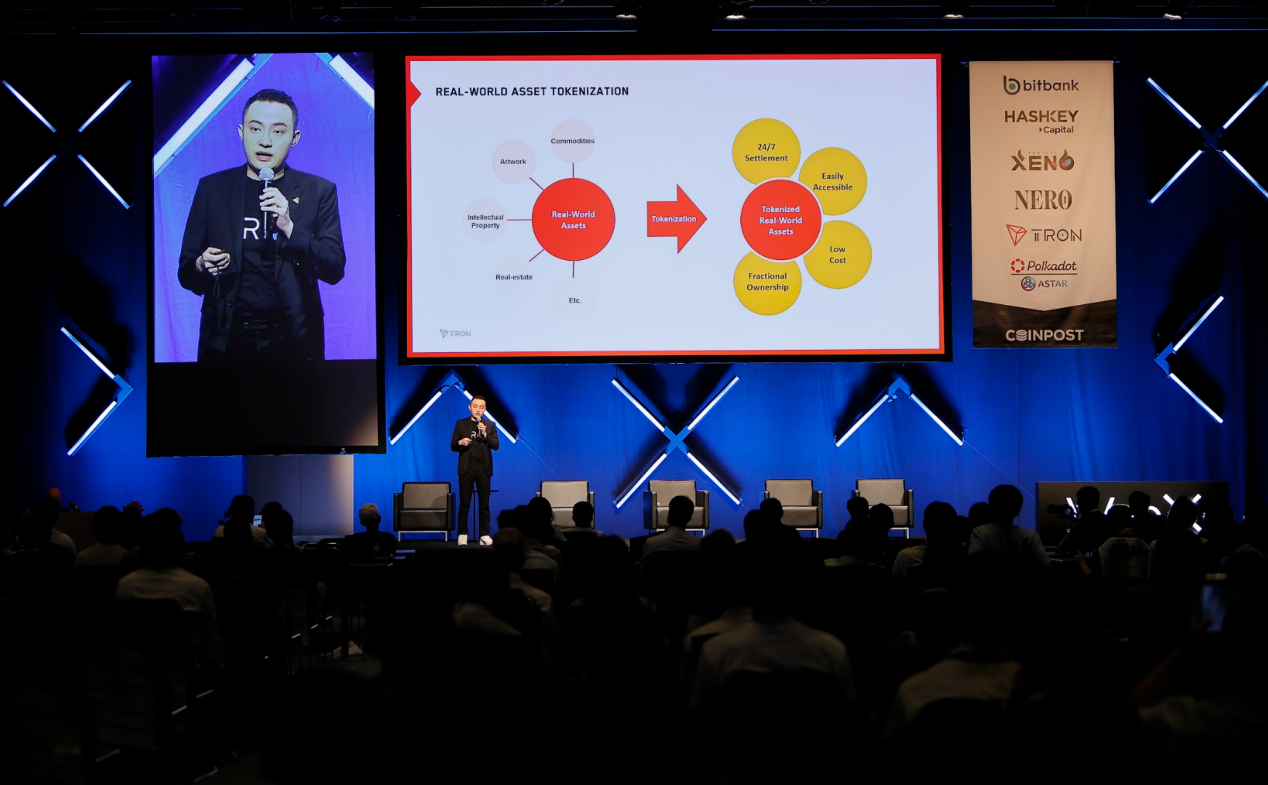
但有些NFT并不可转让，而且毫无价值，例如许多可重复使用的KYC提供商发行的灵魂绑定代币。此外，NFT并不总是必须代表数字对象，随着不可替代的RWA寻求利用区块链，NFT通常可以作为数字孪生体，代表从交易卡到奢侈手袋的一切。

与其他区块链标准一样，NFT既受益于区块链的开放性，也受益于作为标准的一致性。它们是可移植的，可以随用户移动到任何应用程序。反过来，该应用程序要能够理解什么是NFT，并对其采取行动，从而进一步扩展其实用性。这也意味着，对于任何发布的NFT，都可以立即访问为该标准构建的所有现有工具。一般而言，这意味着任何NFT都可以立即在交易所交易、借用或捐赠。

区块链数据的可组合性和开放性以及扩展的NFT拥有巨大的潜力，但也并非毫无弊端。它们可以提供新颖的体验，并使应用程序能更详细的了解用户，但市场目前所构建的系统仍处于以保护隐私为主的早期阶段。它们可以允许透明和程序化的价值转移，如铸造费或版税，但也可以允许应用程序绕过这些规则（版税对创作者来说是一个福音，目前新的生态系统正选择在NFT标准水平上强制执行版税）。