“一次性空投”不靠谱?如何改进加密项目的代币分发方式
来自 | Zee Prime Capital
作者 | @Luffistotle
编译 | Jordan,PANews
加密市场里经常会有各种空投活动和相关宣传,但我们建议每个Web3项目都该重新考虑一下协议的代币分发方法。
代币空投并不是一个明智的策略,对大多数加密项目而言,除了“5分钟热度”之外,空投其实并不会带来更多积极效果。有时候,空投活动一结束,项目似乎就有一种“是时候甩掉我的责任”的感觉,所以想要获得长期成功,单靠“免费赠品”肯定行不通。如果你的目标是要让项目资产随时间推移变得越来越有价值,那么进行的每一次空投都像是在挖一个“原生资产贬值的洞”,这个“洞”挖的越深,填补的金融资本就会越多。
实际上,项目之所以要给加密社区分发代币,目的很简单,就是为了获客。也许很多人并不知道,Web2科技巨头的大部分工作是去“做销售”,但就现阶段来看,Web3领域里的很多项目似乎并不重视“销售”,许多销售业务模型看起来也非常“懒惰”。
在Web2领域里,一些高速增长的科技巨头主要关注两个获客基本模型,一个是客户获取成本(CAC),另一个是客户生命周期价值 (CLV)。对于Web3项目来说,每次空投赠送代币都类似于Web2公司的营销支出,即付出了客户获取成本,而客户生命周期价值则是用户通过使用平台带来的经济回报(例如协议收入)的总和。对于传统科技公司而言,如果“CLV/CAC”的值越大,就意味着市场竞争力越强,投资方就愿意“烧钱”,如果投资者没有看到这种长期价值,他们就会改变策略,比如降低客户获取成本,提升客户生命周期价值等,其实Web3项目也可以这么做。
简单来说,当“客户生命周期价值”大于“客户获取成本”时,你就能赚钱,反之则会赔钱。此外,投资回报周期也很重要,对于投资者而言,他们肯定希望自己的投资回报时间越短越好,最好能在12-24个月内收回投资成本,而不是等待5-7年。
(注:上面所说的这些概念,有些可能会对Web3项目有所帮助,但有些确实对Web3项目没有太多作用。)
在Web3领域里,如果你希望自己“空投的代币”能够扮演“客户获取工具”的角色,那么对于一个在起步阶段几乎不赚钱的Web3项目来说(此时你的客户生命周期价值很低),随便制定一套空投策略并可取。一般来说,作为协议所有者,你的目标应该是将代币尽可能地空投到合适的人手中,他们未来会使用你的应用程序,也会转变成拥有较高生命周期价值的客户;如果你过早地把全部/部分代币空投给了错误的人,他们未来不仅会抛弃你的产品,更不可能转换成高生命周期价值的用户,你也很难再构建出更多契合市场的产品。
在传统证券市场里,人们之所以会购买、持有股票和股权,是因为他们相信自己可以获得未来现金流的权利,买到一个有潜力的股票/股权会给他们带来可预见的价值,因此这种股票和股权就很有吸引力。代币其实也算是一种与股票类似的投资工具,如果你仅推出一个没有价值的治理代币,意味着持有者无法真正获得“有形利益”(tangible benefits),因此只要这个代币价值大于零,持有者肯定会义无反顾地选择抛售而不是长期持有,毕竟拿着毫无价值的治理代币只是为项目的早期投资者和团队创造流动性事件,反而自己无法获得太多利益。(当然,项目团队肯定希望持有治理代币的人越多越好)
学过微观经济学的人都非常清楚一个道理:任何一种商品的价格都是由供需关系决定,如下图所示:
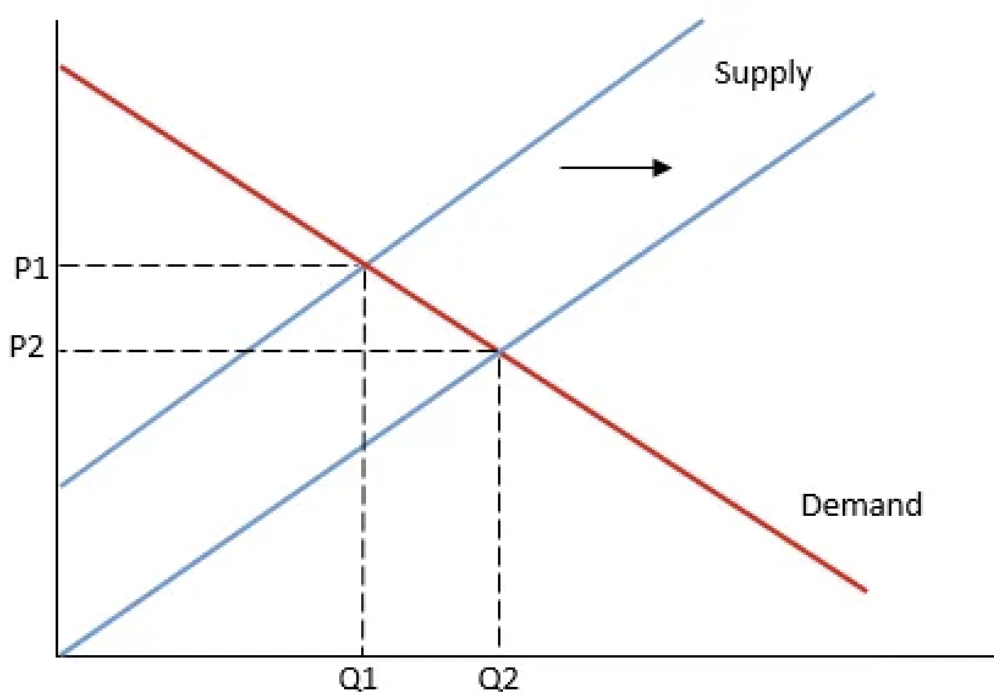
如果你无法为代币创造需求(在现阶段的加密市场,意味着要创造让更多人持有的需求)而仅仅是不断增加代币供应量,结果可想而知。虽然价格不代表一切,但正如我们之前在许多协议叙述中看到的那样,价格肯定是一个非常重要的因素。
那么,我们该又如何改进代币分发策略呢?
一、空投
免费代币空投不应该是“一次性”行为,坦率地说,我已经从过去大量代币空投实例中看到不少糟糕的结果。韩国风险投资公司Hashed研究员cpt n3mo对“一次性代币空投”做了量化分析,结果发现在不同时间范围内,价格中位数都显示出极差的表现,比如空投100天后,代币平均价格表现下跌了36%,因此很难说代币被投放到“合适的人”手中。虽然一次性空投代币能够引导社区并吸引更多早期参与者,但如果从长期发展角度来看,这种方式似乎效果不佳。
不过,免费代币空投的确能对参与者心理产生影响(想想禀赋效应,当个人一旦拥有某项物品,那么他对该物品价值的评价要比未拥有之前大大提高),而且项目也可以将代币锁仓释放期范围拉的更长一些,通过提供这样的代币分发机制,空投参与者可以获得更多好处。虽然从套利角度来看,能够参与到早期空投的用户的确能获得更大利益,但如果将“空投活动”变成一种连续行为,也未尝不是件好事。
“一次性空投”还有一个负面影响:新用户会觉得自己错过了一个生态系统、一个好机会,这反而对损害采用率,因为新用户会觉得“哦,空投已经结束了,了解那个生态系统已经没有意义了。”从这个角度来说,Web3项目其实可以通过“放长线”的形式来激励早期支持者,而不是一次性空投代币后就不闻不问了。但最根本的转变,还是要将空投性质变成权证性质,将激励过程从离散性变成连续性,Optimism就是一个好例子,他们的激励措施是多阶段的,尽管持续时间较长,但至少朝着正确方向迈出了重要一步。
那么,如何才能实现“持续性”呢?答案其实很简单,就是让新参与者成为生态系统的重要组成部分(参与新产品、治理等),同时让他们能够获得与老用户相类似的好处。项目不能因为用户参与时间较晚就不让他们获得“福利”,更不要说许多新用户其实能给项目增加更多价值——你要做的,应该是吸引能给项目带来最大价值的用户,而不是最早入场的用户。
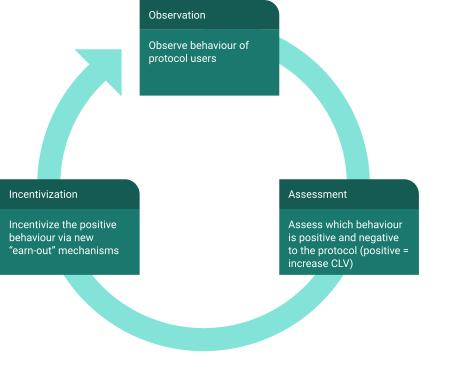
为用户提供“可持续福利”,还可以提高项目对生态系统的动态和反思能力,代币发放标准还可以根据用户积极行为、或是消极行为进行调整。作为协议所有者,你设计的空投策略必须要能影响生态系统参与者的行为,影响力越大越好。
二、设计社区代币分发机制
如何构建社区代币分发机制?一个有趣的方法是设计“游戏化KPI”,利用KPI机制来调整代币分发率。Zee Prime Capital目前正在探索一种创新方式,旨在将协议愿景和社区回报保持一致。
举个例子,你可以针对收入指标来调整代币释放率,确保代币持有者在项目采用阶段能获得利润,让客户生命周期和项目成功周期保持一致,客户生命周期扩展越大,成功周期就越长(你可以参考传统企业的生命周期发展路径和盈利能力之间的关系)。
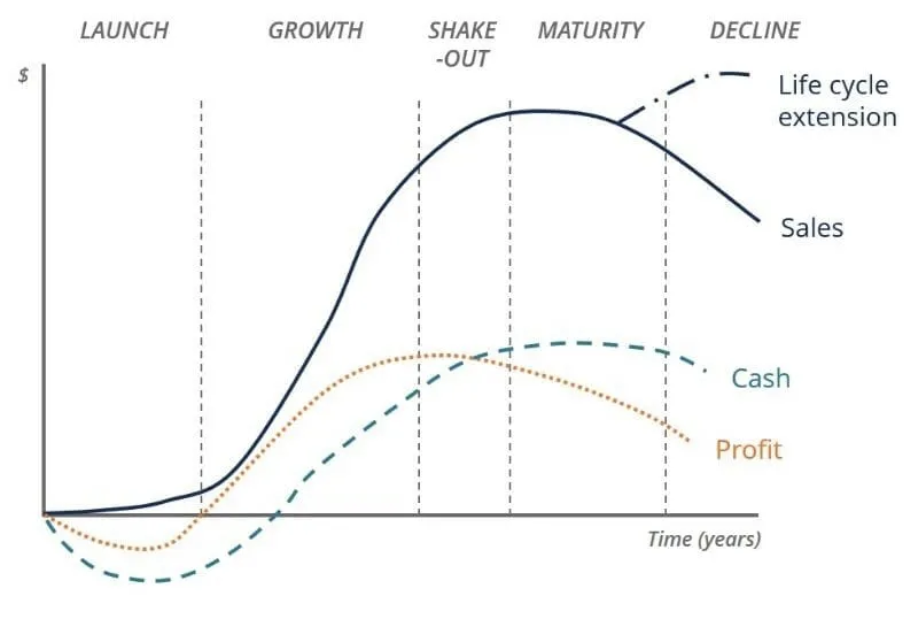
不仅如此,你还可以自己设计一条“辅助线”来追踪利润指标,然后与代币释放时间匹配起来,从某种意义上来说,这样就能将价值“推回”给用户,而不是锁定在协议金库中。理论上,这种做法还能产生良性循环并延长生命周期。
三、探索具有创造力的代币分发方式
任何代币分发方式都伴随风险,这点不言而喻。一个已知的验证标准是开放女巫攻击,但降低风险的最佳方法可能依然要不断优化改进代币分发标准,以便将成本降低到可接受的滑点水平,而不是仅仅依赖于传统空投的实际收益。
因此,我们需要对项目的代币分发方法进行创新,比如允许修改代币分发策略,给那些等待更长代币释放时间的用户提供更多折扣优惠。简单来说,在探索代币分发方式创新的时候,最重要的就是要有创造力。
在这方面,目前加密市场上一个值得关注的示例是Brahma Finance的KARMA系统。KARMA是一个(灵魂绑定)积分系统,用户在社区内努力做出贡献就能获得奖励,但会根据活跃程度提供激励措施,如果你不是一个社区积极分子,那么奖励积分可能就会减少。如果你能拿到更高的KARMA积分,那么就有权访问协议上的特殊金库并获得其他利益(比如购买稀有商品、访问优惠活动)。目前Brahma Finance即将推出KARMA V2,旨在将这套系统推广到更多其他协议。
Brahma Finance的KARMA V2将会是一个针对高级用户的持续奖励系统,与直接股权补贴相比能够显着降低用户获取成本,团队可以根据KARMA分数来添加“折扣代币”或“免费代币”等选项,其系统管理功能也能帮助项目更好地规划代币释放计划,比如是否需要调整代币释放量和释放时间来匹配协议价值。
随着Web3“社交挂毯”(social tapestry)变得更加丰富多彩、Sismo (类似于灵魂绑定代币等)等去中心化私人认证提供商和各种有趣的指标(比如Degenscore)越来越多,项目可以更好地定位到自己最想要的受众群体。
总结
总之,一个较好的币分发模型应该有以下几个特点:
1、让用户能以折扣价购买的应该是“认股权证”而不是“空投代币”;
2、通过可持续性流程,项目能在更长的时间范围内奖励用户;
3、制定可修改的动态标准;
4、设计、试验更具创造力的代币分发机制
事实上,早在2017年,Coinbase联合创始人Fred Ehrsam就在自己的博客中提到过类似的观点,希望项目可以将自身发展价值与用户追求的激励保持一致:
“协议设计者需要思考如何设计区块链的进化特征——具体来说,设计出一套让更多人加入的经济激励模式,然后不断优化、改进它。”
Fred Ehrsam说的没错,任何一个加密项目/协议的最高目标,就要“对齐”自身价值与用户利益,而这也是转动项目/协议长期成功发展的飞轮。去中心化代币系统的出现,让我们看到这一目标可以成为现实,但我们也需要仔细思考,努力让项目自身价值和用户利益保持一致。
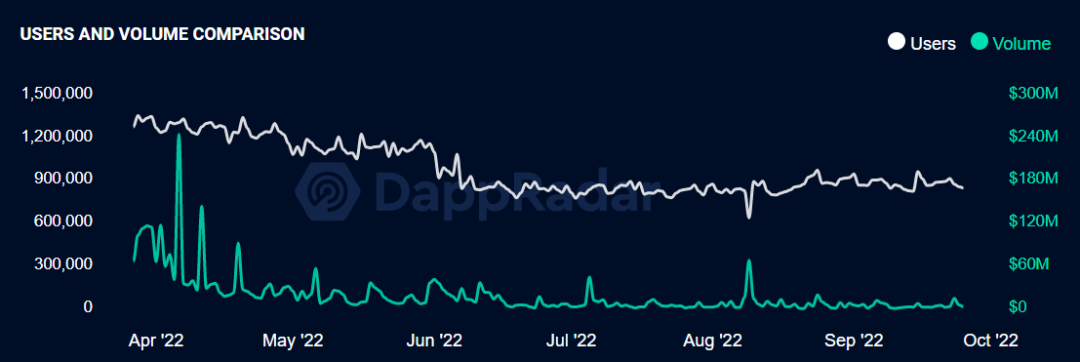
与此同时,仅仅利用去中心化代币系统并不能保证实现“自身价值和用户利益保持一致”的目标——99% 的加密项目已经证明了这一点,毕竟大多数代币的发展轨迹都类似于下面这张图表(该图所展示的代币价格走势是不是似曾相识):

所以,我们应该突破界限,帮助加密项目创造构建出更好的代币分发方式。