5分钟读懂Elixir:模块化DPoS网络,为何入了Arthur Hayes的“法眼”?
作者:念青,ChainCatcher
编辑:Marco,ChainCatcher
近日,模块化 DPoS 网络 Elixir 宣布完成 800 万美元 B 轮融资,Mysten Labs 与 Arthur Hayes 的家族办公室运营的 Maelstrom Capital 联合领投,Manifold、Arthur Hayes、Amber Group、GSR、Flowdesk 等参投。
据 RootData 页面显示,Elixir 成立于 2022 年,是模块化 DPoS 的流动性网络,使任何人都可以直接向订单簿提供流动性,为长尾加密资产带来流动性,允许交易所和协议引导其账本流动性。Elixir 分别于去年 1 月和 10 月,完成 210 万美元种子轮融资和 750 万美元 A 轮融资,投资方包括 Hack VC、NGC Ventures、FalconX 等知名机构。
除了屡获融资的消息外,Elixir 一直在中文社区比较低调,关注度并不高,一个主要原因是,与 dYdX、Vertex 等订单簿 DEX 不同的是,Elixir 是为这些 DEX 项目提供流动性的网络和基础设施,此前推出的两版测试网与用户直接交互的场景并不多。
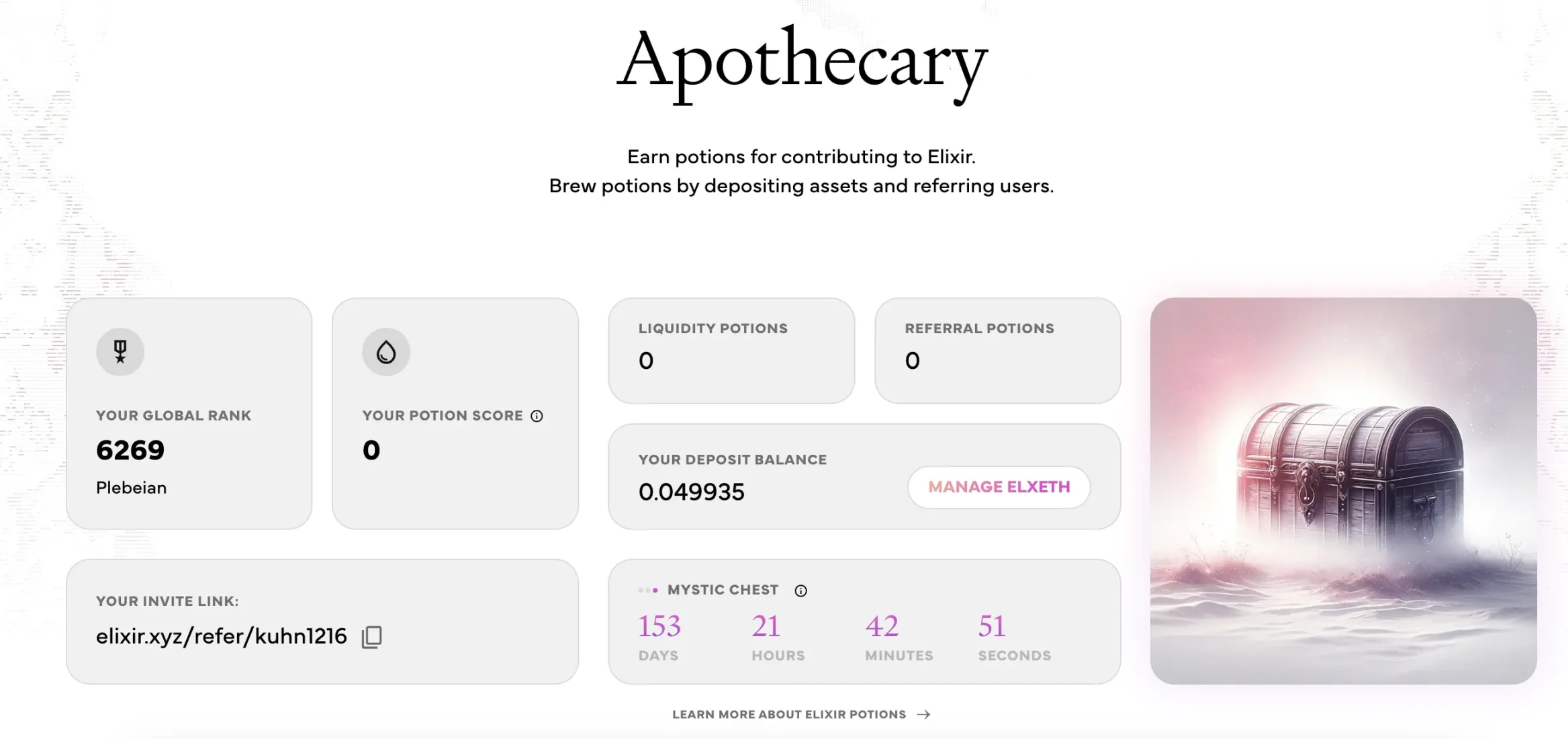
不过,Elixir 近日除了披露了新一轮融资,还宣布推出新产品 Apothecary(药剂师)。Apothecary 是一个新的积分追踪体系,支持用户通过存入资产和拉新来赚取一些积分(potions)/ 收益,帮助用户在今年 8 月 15 日推出主网之前跟踪对网络的贡献。
Elixir 有何亮点?
传统金融市场长期以来依赖中心化中介机构提供流动性,这些机构和对冲基金通过先进的交易策略和算法为交易所优化流动性,然而,将资金委托给中心化机构存在一定的风险。因此 DeFi 一直在探索去中心化订单簿模式,所谓的订单簿模式就是使交易者能够直接相互交易,依赖数学模型和流动性池来促进代币对的交易。
理想状态是,订单簿既能改善目前 AMM 资金效率低、滑点大等问题,又能保证交易的灵活性和资产的去中心化。实际上,订单簿 DEX 更适用于比特币、以太坊等存在大量通证的市场,但面对一些流动性不足的市场和供需深度不足的长尾资产,会出现价差过高而无法成交的问题。
据官网介绍,Elixir 的目标是让任何人都可以直接向订单簿提供流动性,为长尾加密资产带来流动性。这一设想如何实现?Elixir 网络面向散户(也包括机构和做市商)开放交易对,并对 APY 进行补贴,更高的收益自然吸引更多用户来通过网络直接向订单簿提供流动性。Elixir 可与其他项目跨链组合,订单簿 DEX 能够将 Elixir 集成到其核心基础设施中。
一方面订单薄 DEX 就可以共享 Elixir 作为基础设施带来的流动性,提升交易体验;另一方面,普通用户很难在订单薄 DEX 提供流动性,只能手动挂单交易,用户通过 Elixir 就可以自动高频的挂买单卖单,赚取流动性费用。这样一来,用户在使用订单薄 DEX 就像 AMM 一样,可以比较便捷地提供流动性。
从网络架构上看,Elixir 运行的订单簿与 Uniswap v2 的 x*y=k 曲线几乎等效,这一曲线用于建立流动性并能缩小订单簿上的买卖价差,与 AMM LP 具有非常相似的风险和回报。网络对交易所下的订单达成 DPoS 共识。
此外,其基础设施类似于 Arbitrum 的安全模型,欺诈证据发布在以太坊主网上。值得一提的是,Elixir 还集成了各个交易所的公开数据(包括中心化交易所),保证交易、头寸和订单簿的低延迟更新和跨交易所订单簿的一致。
在生态方面,Elixir 生态已与 30 多个 DEX 集成。因为订单簿模式需要廉价且高频的交易,所以对区块链的吞吐量有很高的要求。这些项目多为 Sui、Sei、Starknet、Arbitrum、Blast、Injective 等具备高吞吐量且低 gas 费的 L1、L2 网络生态中的交易所,包括 Vertex、RabbitX、NFTPerp、Orderly Network、dYdX 等。
目前,Elixir 网络已计划发行代币 ELX,但尚未公布代币经济模型。据介绍,ELX 主要有两个用途,一是用于节点和验证者质押,保证网络安全,二是用来做为社区治理代币。
用户可以做哪些交互?
Elixir 成立于 2022 年,目前已经上线了两版测试网,并即将开启 v3 测试网,这也是 8 月主网上线前最后一个测试网。目前用户可以通过运行节点、赚取积分、为与 Elixir 集成的 DEX 提供流动性等方式交互。
1、运行节点 / 验证器
目前,Elixir 已在全球拥有 13563 个节点,用户可通过运行节点获取奖励。不过,官方已经暂停了测试网 v2 的节点申请,正为 v3 的发布做准备。用户可以在 v3 上线后再申请运行节点。
相关链接:https://docs.elixir.xyz/running-an-elixir-validator
2、Apothecary:赚取积分
Elixir 于 3 月 12 号推出的新产品 Apothecary 实际上是一套比较系统的积分追踪工具,可以追踪用户对网络的贡献、集成、铸造 elxETH 以及拉新等,此外,运行节点和在与 Elixir 集成的交易所进行交易也可以赚取积分(potions)。
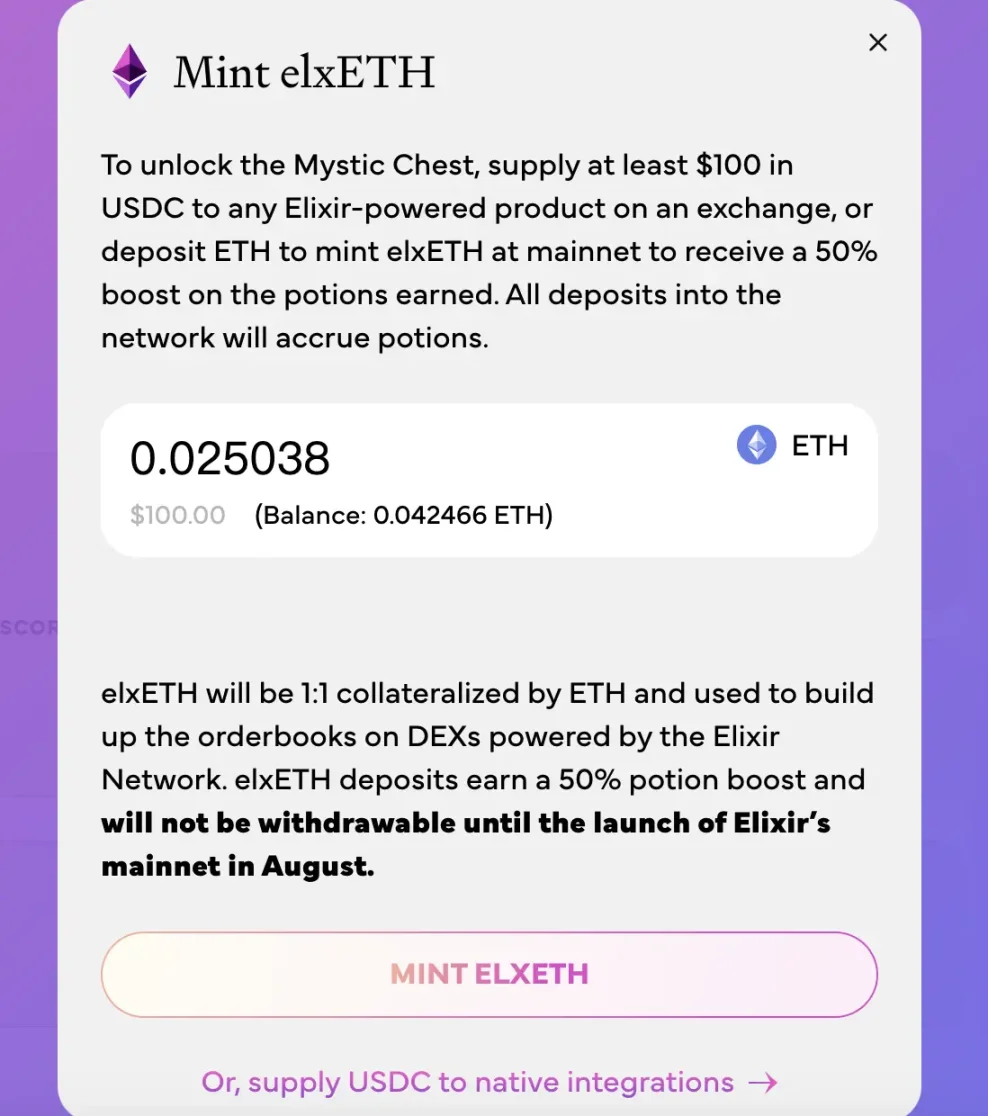
如图所示,用户可以存入至少价值 100 美元的 ETH 来铸造 elxETH 来解锁神秘宝箱。elxETH 是一种以 ETH 1:1 比例支持的原生收益代币,主网启动后将成为全链 LP 代币,为交易所的订单簿流动性提供动力。存入的资产将被协议锁定,并为 Elixir 支持的产品和 DEX 提供流动性。8 月 15 日主网上线后,用户将能够提现,并解锁宝箱获取收益,如果选择不提现,那这笔资产届时将自动从交易所赚取奖励。
资产的多少决定了积分的数量,此外邀请新用户存入资产也能赚取积分。
相关链接:https://www.elixir.xyz/apothecary
3、为与 Elixir 集成的 DEX 产品提供流动性
用户也可以通过在 Elixir 生态的交易所上存入大于 100 美元的资产赚取积分。但是相比之下,在主网铸造 elxETH 可以多拿 50% 的积分。
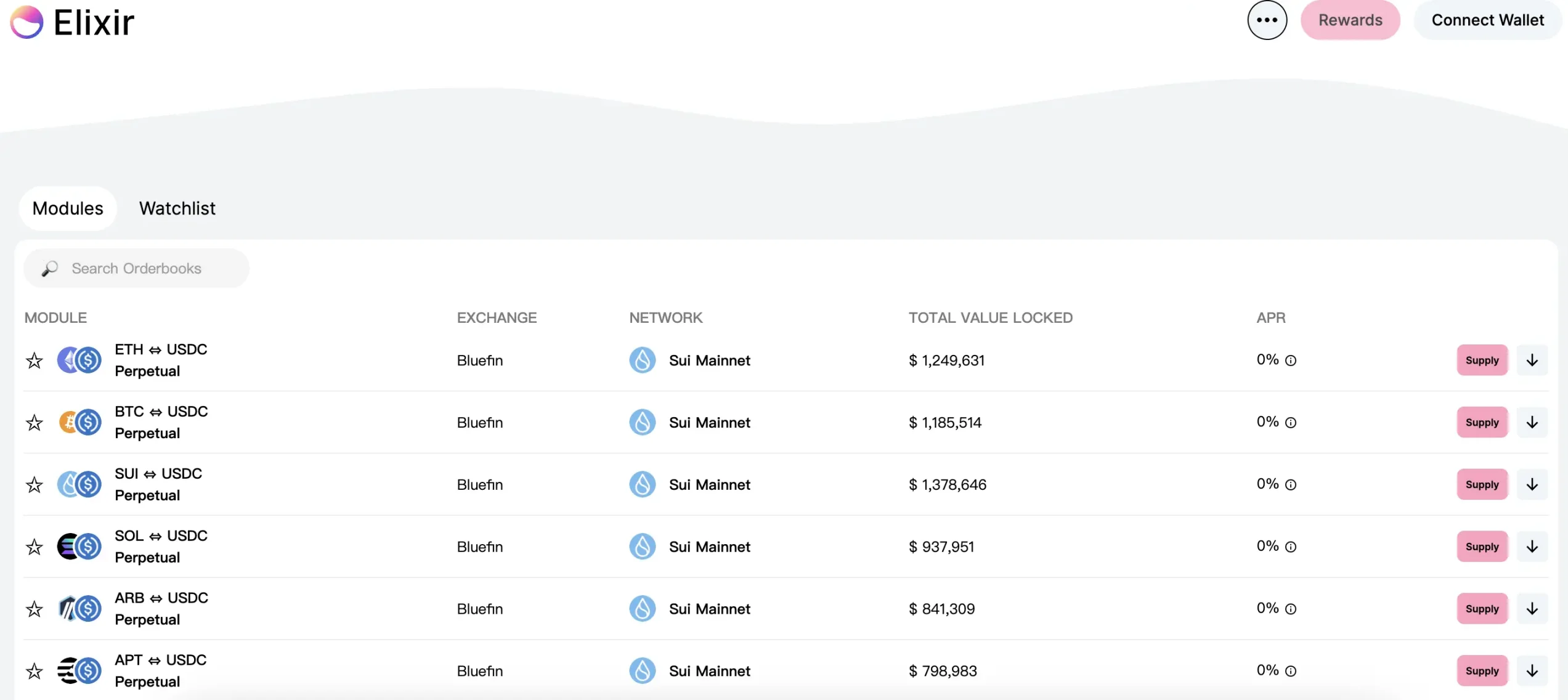
Elixir 目前支持 Bluefin 上超过 50% 的订单簿流动性 、Vertex 上超过 20% 的订单簿流动性、RabbitX 上超过 40% 的订单簿流动性,此外还即将推出的原生集成包括 dYdX、Hyperliquid、Orderly 等其他 30 多种。
相关链接:https://agg.elixir.xyz/