Move智能铭文爆火后，SFT还能有哪些创新玩法？

作者：菠菜菠菜

Move 智能铭文的爆火后，SFT (Semi-Fungible Token) 半同质化资产赛道即将在牛市爆发？SFT 类型资产还能有哪些创新玩法？

SFT 如何给各赛道带来新创新空间？为什么在这轮牛市必须关注 SFT 赛道？

菠菜来讲讲到底什么是 SFT 以及 MOVE 铭文爆火现象下 SFT 资产赛道还存在哪些潜在的机遇。

继上次菠菜利用 Move 智能铭文 SFT 的特性搞出理论「万倍收益」后，MoveScriptions 团队立马就上线了官方交易市场。

项目方选择了根据 amount 单价进行排序而不是铭文本身，这种机制非常适合 SFT 资产的交易，避免了 NFT 交易逻辑的尴尬情况。

同时很多小伙伴也在问什么 SFT？

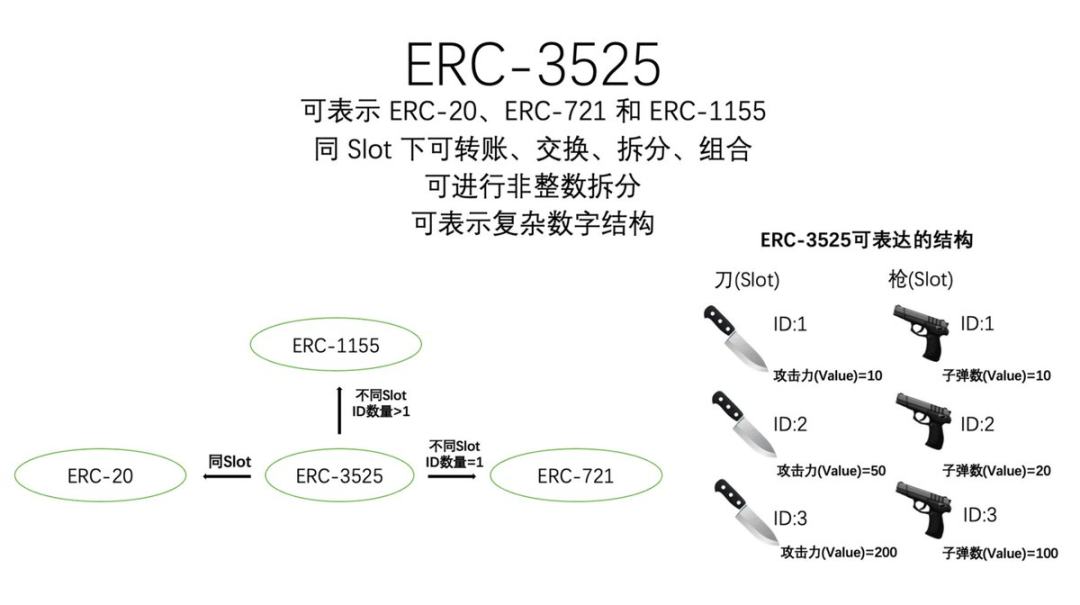
SFT (Semi-Fungible Token) 半同质化代币起源于以太坊的 ERC-3525 标准，于 2022 年 9 月正式通过称为以太坊新的代币标准，一经通过备受关注，不仅在于它是最底层的创新，而且还是由我们华人团队 Solv Protocol 主导设计的一个标准。

但由于诞生于熊市，其巨大潜力一直未能得到大量关注，潜力十分巨大！

SFT 简单来说，你可以把 SFT 理解为是 NFT 和 FT 的结合，是一种超级 NFT，可以拆分组合，但是又比 NFT 和 FT 具备更高的创新空间和组合性，还具备一些特有的特性，比如「容器」性质以及现金流编程能力。

想了解更多技术细节可以翻菠菜以前的文章，总而言之 SFT 可以做一些复杂结构的资产，特别适用于金融、游戏领域。

SFT 具备的容器能力从 MOVE 铭文中可以得到充分的体现，每铸造一个铭文都会往里面锁定铸造费等额的 SUI，可以烧毁随时取出回本，而烧毁后也会造成一定的通缩。

这种机制使得其一级参与者几乎不会亏钱，只需要花费可忽略不计的 gas 成本就可以获取潜在的高额收益，不会归零的特性也给了许多人参与的动机。

当看到 @jolestar 使用 SFT 结构开发的 MOVE 铭文协议取得了如此火爆的热度后，菠菜也是十分高兴，也陆续写了两片推文介绍 SFT 的技术优势，当然菠菜不会鼓励大家去炒 MOVE 铭文，不作任何投资建议，DYOR。

菠菜也借此事件跟大家聊一聊 SFT 还可以有哪些创新玩法？有什么新叙事？目前 SFT 生态到底怎么样了？

首先简洁介绍一下目前 SFT 生态情况，在现实世界方面，我们官方孵化了与三个国家央行合作的使用了 ERC-3525 的项目，并将在未来持续与这些权威机构持续推进 Web3 技术在真实世界的应用。

在 Crypto 领域，DeFi 领域做链上基金业务的 Solv 成为了去中心化资管赛道的龙头，已经突破上亿美元的资产发行规模。

在 GameFi 领域，若干项目方使用 ERC3525 做了一些创新玩法，比如结合 AI 使得 NPC 可以与玩家进行资产交互；利用 SFT 的特性打通多游戏类型的积分共享。

在 DePIN、SocialFi 领域也有若干项目方了结合 ERC-3525 的优势去增强项目的竞争力。在现代密码学的领域，SFT 与现代密码学的结合也产生了一些奇妙的化学反应。

当然 SFT 的想象空间不止如此，菠菜也提一些自己的 SFT 潜在的玩法：

一、全自动分红协议

SFT 的一个非常重要的特质就是可以对现金流进行编程，大白话就是钱的流动都可以在一个智能合约内进行管理，举一个案例说明：项目方可以将自己未来部分的现金流收益提前出售进行融资，让用户与项目方共担风险。

这种模式其实在国内传统金融圈已经在跑了，就是将中小微企业未来现金流作为金融产品的「滴贯通」，但是链上实现会更有优势，一切由智能合约自动执行。

项目方只需要将分红合约与项目合约进行结合或手动打入分红合约，SFT 合约就会自动根据持有者的份额分发给所有 SFT 持有者，不需要管份额如何流通。

在这轮牛市中这种出售未来现金流的融资方式或许会大放光彩，甚至出现一些骚玩法，比如某兮发一个 SFT 资产向大家融资去炒合约，赚了钱分给大家。

二.Web3 粉丝 / 创作者经济

FriendTech 的爆火也让许多人开始关注 SocialFi 这个赛道能有什么样的新玩法，SFT 其实提供了一个更灵活的资产结构。

怎么通过区块链将粉丝之间的关系进行通证化进行链接一直是 SocialFi 赛道探索的方向，传统使用 NFT 和 FT 的手段虽然在技术上可行，但想实现某些操作的话会大大增加技术复杂性。

例如不同的创作者 / 房间都需要发行一套 NFT 合约分发给粉丝，如果想结合别的创作者一起合作给粉丝发福利的话，技术上就会很麻烦。

由于 SFT 既可以表达 NFT 也可以表达 FT，而 SFT 又可以在一个合约里发行多种类型的「NFT」，不同类型之间既可以相互交互也可以无法交互，在设计上有着很大的灵活空间，这样避免了多次部署合约的冗余，也更容易实现一种「Open Loyalty」的叙事，即不同的组织之间可以共享其忠诚度计划合作共赢带来更多价值。

而利用其自动分红的特性，通过 SFT 自动根据粉丝的贡献度分配利益也是一个非常大的优势。

三、一种全新的 DAO 治理范式

这个想法纯属开脑洞，在许多 DAO 治理的过程中，很大程度的矛盾来自于利益分配机制，基于铭文公平发售以及自动分红的机制，是否会诞生一种全新的治理结构？

比如通过发行智能铭文筹资成立一个 DAO，早期 DAO 成员根据贡献的资金量决定早期利益分配机制，并设计一些机制去激励未来的贡献者，当然这块内容只是开个脑洞，留给大家去讨论。

四、资产嵌套组合玩法

由于 SFT 具备「容器」的特质，理论上是可以实现多层资产嵌套的，就像俄罗斯套娃一样，无穷嵌套。

比如 SFT 里装着一个 ETH，或 SFT 里装着一个 SFT？SFT 里装着一个装着 SFT 的 SFT？需要另外一个 SFT 燃烧才能解锁拿出里面资产的 SFT？想象空间很大，留给大家去思考。

总而言之，市场普遍有着这轮牛市缺乏创新缺乏叙事的说法，SFT 的想象空间远不如此，这轮牛市难道你还不关注 SFT 赛道？

声明：以上内容均个人观点，不代表任何官方立场，投资 MOVE 智能铭文需谨慎，DYOR，希望大家能从技术角度可以找到更多创新的想法，欢迎一起加入共建！