模块化区块链Celestia发币,速览空投细则及代币经济
来源:Celestia
编译:Karen,Foresight News
今日,模块化区块链 Celestia 宣布将发布原生代币 TIA,并启动创世空投 Genesis Drop。创世空投对象包括7,579 名开发者和以太坊 Rollups、Cosmos Hub 和 Osmosis 上的 576,653 个链上地址,空投遍布开发者、生态项目贡献者、普通用户、质押者等。
Celestia 是一个基于 CometBFT 和 Cosmos SDK 的权益证明区块链。Celestia 支持协议内委托,并且将从 100 个初始验证器集开始。作为验证者或委托者质押 TIA 将能够从网络中获得质押奖励。验证者也能向委托者收取一定的费用,从而获得一定比例的质押奖励。
那 Celestia 原生代币 TIA 有何效用?代币经济学和释放规则是怎样的?空投标准又有哪些?
TIA 有何效用?
其一,TIA 是开发人员构建模块化数据可用性网络的重要组成部分。为了使用 Celestia 实现数据可用性(DA),Rollup 开发人员在网络上提交 PayForBlobs (PFB) 交易,需要以 TIA 形式支付一定费用。
第二是,与基于以太坊的 Rollups 上的 ETH 类似,除了为数据可用性付费之外,开发人员还可以选择使用 TIA 作为 Gas 代币来快速启动他们的链。在这种模式下,开发人员可以专注于创建应用或执行层,而不必立即发行代币。
最后是质押和网络治理功能,作为使用 Cosmos SDK 构建的无需许可的网络,Celestia 使用权益证明来确保共识。与其他 Cosmos 网络一样,任何用户都可以通过将其 TIA 委托给 Celestia 验证者来获得验证者的部分质押奖励,从而帮助保护网络安全。TIA 还允许社区从第一天起就在 Celestia 关键部分的去中心化治理中发挥关键作用,例如对网络参数进行投票和管理社区池。
社区池中,从网络启动开始,Celestia 的社区池将获得所有 Celestia 区块奖励的 2%。TIA 持有者可以投票从社区池中支出 TIA 并资助生态系统计划。
TIA 代币经济学
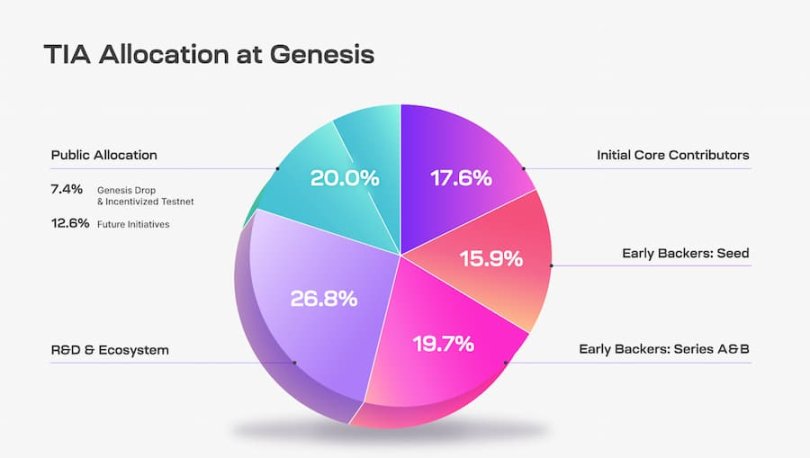
TIA 创世总供应量为 10 亿枚,具体分配方式为:
- 公开分配 20%(7.4% 为创世空投和激励测试网分配,12.6% 为未来激励分配),这部分发布时完全解锁;
- 26.8% 分配给分配给 Celestia 基金会和核心开发人员用于研究、开发和生态系统计划(发布时解锁 25%,剩余 75% 从第 1 年到第 4 年解锁;
- 15.9% 分配给种子轮早期投资者(33% 在第一年解锁,其余 67% 从第 1 年到第 2 年解锁);
- 19.7% 分配给 A 轮和 B 轮的早期投资者(33% 在第一年解锁,其余 67% 从第 1 年到第 2 年解锁);
- 17.6% 分配初始核心贡献者(33% 在第一年解锁,其余 67% 从第 1 年到第 3 年解锁)。
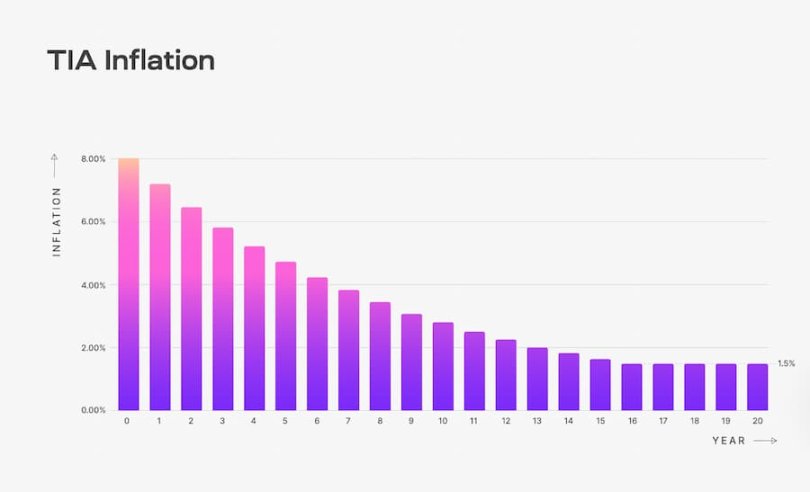
TIA 通胀率从每年 8% 开始,每年下降 10%,直到达到 1.5% 的长期发行率。确切的年通货膨胀率如下图所示。
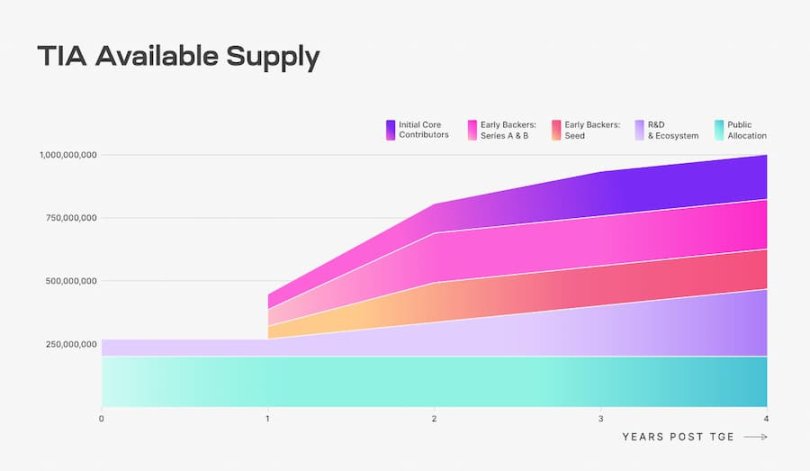
代币释放和供应量变化方面,Celestia 在创世时的 10 亿枚 TIA 供应量将受到几个不同的解锁时间表的约束。所有锁定或解锁的代币都可以被质押,质押奖励在收到后即被解锁。
Celestia 创世空投
Celestia 创世空投将分配给 7579 名开发者,以及以太坊、Rollups、Cosmos Hub 和 Osmosis 上的 576,653 个链上地址。空投认领将于 2023 年 10 月 17 日 20:00 结束。创世空投结束时,无人认领的代币(最多 4500 万个 TIA)将分配给已提交地址的开发者和账户。
值得注意的是,美国或其他被禁止司法管辖区的用户无法领取空投。
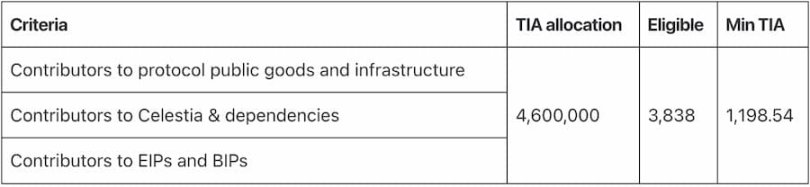
一、研究和公共产品(分配 600 万枚 TIA)
其中,研究和公共产品分为协议公共产品和基础设施(460 万枚)和 Eth Research 社区(140 万枚)。
协议公共产品和基础设施的资格标准为:
- 协议公共产品和基础设施的贡献者;
- Celestia 的贡献者和依赖项;
- EIP 和 BIP 的贡献者。
Celestia 还将向 Eth Research 论坛的成员分配 140 万枚 TIA,具体资格标准为:
- 在 2023 年 7 月 5 日之前创建至少 1 个主题或 1 个帖子的 Eth Research 论坛用户(排除了 Celestia Labs 团队成员和顾问)。
二、早期的模块化生态(1400 万枚)
Celestia 将把 835 万枚 TIA 分配给以 Celestia 生态图中的组织贡献者,以及参加模块化峰会 Modular Summits 1 和 Modular Summits 2 的组织的公共贡献者,以及 Celestia 模块化研究员计划第 1 组的参与者(也排除了 Celestia Labs 团队成员和顾问)。
额外的 565 万枚 TIA 将分配给在所有合格存储库中总共至少有 4 次提交的 Github 超级贡献者,更多的 TIA 分配给在研究和公共产品以及早期模块化生态系统标准中总共至少有 23 次提交的贡献者。
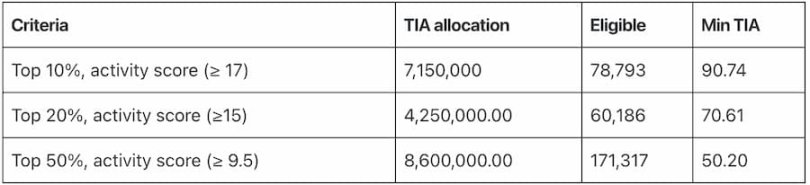
三、以太坊 Rollups 的早期采用者(2000 万枚)
以太坊 Rollups 的早期采用者将获得 2000 万枚 TIA 奖励,会分配给 L2Beat 上 TVL 排名前 10 大以太坊 Rollup 的前 50% 活跃用户,快照时间为 2023 年 1 月 1 日(以太坊区块 16308181)。
符合条件的以太坊 Rollup 包括 OP Mainnet、Arbitrum One、Arbitrum Nova、Starknet、zkSync Lite、dYdX (StarkEx)、Immutable (StarkEx)、SoRare (StarkEx)、Loopring、Metis Andromeda。
为了确定用户的链上活动水平,Genesis Drop 会为以太坊和所有符合条件的 Rollup 上的链上行为分配积分。具体的考量因素包括与智能合约和应用程序交互、持有 ENS 域名、捐赠给 Gitcoin、花费的 Gas 以及最近一笔交易等。
这部分空投对象排除 Hop 女巫列表、Hop 的交易 / 中继黑名单、OP 空投 #1 女巫过滤器以及 Trusta Labs 根据其识别链上集群行为和资产转移方法确定的很有可能是女巫的以太坊和 Rollup 地址。
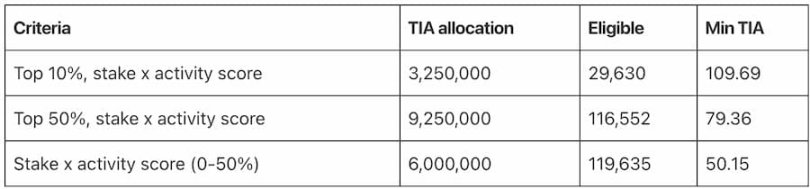
四、Cosmos Hub 和 Osmosis 的质押者和 IBC 中继器(2000 万枚)
Celestia 将把 1850 万枚 TIA 分配给 Cosmos Hub 和 Osmosis 质押者和委托人( ≥ 75 美元),邀请他们加入 Celestia 并参与保护和管理网络。快照发生在 2023 年 1 月 1 日之前,即,Cosmos Hub 区块 13482205 处,Osmosis 区块 7592794 处。
分配指标是根据改编自 Trusta Labs 的 MEDIA 评分框架的 Cosmos/Osmosis 评分方法来评估的,衡量标准包括最后一次交易时间、IBC 交易笔数、所有交易的总价值、账户年龄、消耗的 Gas 等。
此外,Celestia 将分配给 IBC 中继器 150 万枚 TIA,标准为 2023 年 1 月 1 日之前进行 MsgRecvPacket 交易的地址。
来源:https://docs.celestia.org/learn/paying-for-blobspace/https://blog.celestia.org/genesis-drop/